هذا الدرس سوف يتناول المفاهيم الأولية التي سوف نحتاجها للدروس المقبلة الأكثر تقدما، سوف نتناول مفاهيم حيز التعريف، رتابة دالة و تعاريف لرسم الدوال .
الدالة العددية
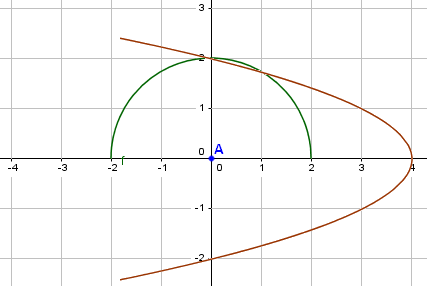
اللون الأخضر يمثل دالة عددية لأن كل عدد x له صورة وحيدة على الأكثر.
اللون الأحمر لا يمثل دالة عددية لأن العدد 0 له صورتان.
نقول أن
$\displaystyle{\displaylines{f}}$ دالة عددية إذا وفقط إذا كان :
$\displaystyle{\displaylines{f:\begin{array}{rcl}I \subset \mathbb{R} & \rightarrow & J \subset \mathbb{R} \\x & \rightarrow & f(x) \end{array}}}$ تطبيق
راجع
درس التطبيقات .
بمعنى أن
$\displaystyle{\displaylines{f}}$ دالة عددية إذا وفقط إذا كان لكل عنصر
$\displaystyle{\displaylines{x}}$ من
$\displaystyle{\displaylines{I}}$ صورة وحيدة في
$\displaystyle{\displaylines{J}}$.
مجموعة التعريف
نعرف مجموعة تعريف دالة عددية
$\displaystyle{\displaylines{f}}$ كما يلي :
$\displaystyle{\displaylines{D_{f} = \{x \in \mathbb{R} \ | \ f(x) \in \mathbb{R} \} }}$ .
مجموعة التعريف تمثل مجموعة انطلاق الدالة حتى يكون لـ
$\displaystyle{\displaylines{f(x)}}$ معنى في
$\displaystyle{\displaylines{\mathbb{R}}}$ .( أي
$\displaystyle{\displaylines{f(x) \in \mathbb{R}}}$ ) .
$\displaystyle{\displaylines{f:\begin{array}{rcl}D_f \subset \mathbb{R} & \rightarrow & \mathbb{R} \\x & \rightarrow & f(x) \end{array}}}$
أمثلة:- نعتبر الدالة : $\displaystyle{\displaylines{ f(x) = \frac{1}{x}}}$ , $\displaystyle{\displaylines{f}}$ لا يمكن أن تقبل صورة في $\displaystyle{\displaylines{0}}$ لأنه لا يمكن القسمة على الصفر . ومن غير ذلك فهي معرفة إذن $\displaystyle{\displaylines{D_f = \mathbb{R}^{*} }}$ .
- الدالة $\displaystyle{\displaylines{f(x) = \sqrt{x}}}$ لا يمكن أن تقبل إلا القيم الموجبة من $\displaystyle{\displaylines{\mathbb{R}}}$ , إذن : $\displaystyle{\displaylines{D_f = \mathbb{R}_{+}}}$ .
- الدالة الحدودية $\displaystyle{\displaylines{f(x) = a_n x^n + .... + a_1 x + a_0 }}$ معرفة على $\displaystyle{\displaylines{\mathbb{R}}}$ , $\displaystyle{\displaylines{D_f = \mathbb{R}}}$ .
- الدالة $\displaystyle{\displaylines{f(x) = \tan(x) }}$ ليست معرفة في النقط $\displaystyle{\displaylines{ x_k = \frac{\pi}{2} + k \, \pi \, / \, k \in \mathbb{Z}}}$ . إذن : $\displaystyle{\displaylines{D_f = \mathbb{R} \smallsetminus \left\{ \frac{\pi}{2} + k \, \pi \ \middle| \ k \in \mathbb{Z} \right\}}}$.
أمثلة:نعتبر
$\displaystyle{\displaylines{h}}$ و
$\displaystyle{\displaylines{g}}$ دالتان عدديتان معرفتان على
$\displaystyle{\displaylines{\mathbb{R}}}$ .
| الدالة | مجموعة التعريف |
|---|
| $\displaystyle{\displaylines{\sqrt{h(x)}}}$ | $\displaystyle{\displaylines{x \in D_{f} \iff h(x) \geq 0}}$ |
| $\displaystyle{\displaylines{ \frac{h(x)}{g(x)} }}$ | $\displaystyle{\displaylines{x \in D_{f} \iff g(x) \neq 0}}$ |
| $\displaystyle{\displaylines{\ln(h(x)) }}$ | $\displaystyle{\displaylines{ x \in D_{f} \iff h(x) > 0 }}$ |
تطبيق : أوجد مجموعة تعريف كل من الدوال التالية.
- $\displaystyle{\displaylines{f(x) = \sqrt{1 - x^{2}}}}$
- $\displaystyle{\displaylines{f(x) = \frac{1}{1+x^2}}}$
- $\displaystyle{\displaylines{f(x) = \sqrt{1-\cos(2 \pi x)}}}$
- $\displaystyle{\displaylines{f(x) = \frac{\sqrt{x-2}}{x^2 - 7x + 10}}}$
- $\displaystyle{\displaylines{f(x) = \frac{1}{|x| - 1}}}$
زوجية دالة
لتكن
$\displaystyle{\displaylines{f}}$ دالة معرفة على تعريفها
$\displaystyle{\displaylines{D_f}}$. لدينا :
$\displaystyle{\displaylines{f}}$ دالة زوجية $\displaystyle{\displaylines{\left\{\begin{matrix}\forall x \in D_f \ : \ -x \in D_f\\ f(-x) = f(x)\end{matrix}\right. \iff}}$
$\displaystyle{\displaylines{f}}$ دالة فردية $\displaystyle{\displaylines{\left\{\begin{matrix}\forall x \in D_f \ : \ -x \in D_f\\ f(-x) = -f(x)\end{matrix}\right. \iff}}$
رتابة دالة
لتكن
$\displaystyle{\displaylines{f}}$ دالة معرفة على حيز تعريفها
$\displaystyle{\displaylines{D_f}}$. وليكن
$\displaystyle{\displaylines{I}}$ مجالا من
$\displaystyle{\displaylines{D_f}}$.
دالة تزايدية
نقول أن
$\displaystyle{\displaylines{f}}$ تزايدية على
$\displaystyle{\displaylines{I}}$ إذا وفقط إذا كان :
$\displaystyle{\displaylines{\forall (x,y) \in I^2 \ : \ x > y \implies f(x) \geq f(y)}}$
نقول أن
$\displaystyle{\displaylines{f}}$ تزايدية قطعا على
$\displaystyle{\displaylines{I}}$ إذا وفقط إذا كان :
$\displaystyle{\displaylines{\forall (x,y) \in I^2 \ : \ x > y \implies f(x) > f(y)}}$
دالة تناقصية
نقول أن
$\displaystyle{\displaylines{f}}$ تناقصية على
$\displaystyle{\displaylines{I}}$ إذا وفقط إذا كان :
$\displaystyle{\displaylines{\forall (x,y) \in I^2 \ : \ x > y \implies f(x) \leq f(y)}}$
نقول أن
$\displaystyle{\displaylines{f}}$ تناقصية قطعا على
$\displaystyle{\displaylines{I}}$ إذا وفقط إذا كان :
$\displaystyle{\displaylines{\forall (x,y) \in I^2 \ : \ x > y \implies f(x) < f(y)}}$
دالة مكبورة - مصغورة - محدودة
لتكن
$\displaystyle{\displaylines{f}}$ دالة عددية مجموعة تعريفها
$\displaystyle{\displaylines{D_f}}$.
- نقول أن $\displaystyle{\displaylines{f}}$ مكبورة إذا وفقط إذا وجد عدد حقيقي $\displaystyle{\displaylines{M}}$ بحيث : $\displaystyle{\displaylines{\forall x \in D_f \quad f(x) \leq M}}$
- نقول أن $\displaystyle{\displaylines{f}}$ مصغورة إذا وفقط إذا وجد عدد حقيقي $\displaystyle{\displaylines{m}}$ بحيث : $\displaystyle{\displaylines{\forall x \in D_f \quad m \leq f(x)}}$
- نقول أن $\displaystyle{\displaylines{f}}$ محدودة إذا وفقط إذا وجد عددان حقيقيان $\displaystyle{\displaylines{m}}$ و $\displaystyle{\displaylines{M}}$ بحيث : $\displaystyle{\displaylines{\forall x \in D_f \quad m \leq f(x) \leq M}}$
مطارف دالة
لتكن $\displaystyle{\displaylines{f}}$ دالة عددية مجموعة تعريفها $\displaystyle{\displaylines{D_f}}$ و $\displaystyle{\displaylines{x_0 \in D_f}}$ و $\displaystyle{\displaylines{I}}$ مجال ضمن $\displaystyle{\displaylines{D_f}}$.
1) القيمة القصوى :
نقول أن العدد $\displaystyle{\displaylines{f(x_0)}}$ هو القيمة القصوى المطلقة للدالة $\displaystyle{\displaylines{f}}$ عند النقطة $\displaystyle{\displaylines{x_0}}$ إذا كان $\displaystyle{\displaylines{\forall x \in D_f \quad f(x) \leq f(x_0)}}$.
نقول أن العدد $\displaystyle{\displaylines{f(x_0)}}$ هو قيمة قصوى نسبية للدالة $\displaystyle{\displaylines{f}}$ عند النقطة $\displaystyle{\displaylines{x_0}}$ في المجال $\displaystyle{\displaylines{I}}$ إذا كان $\displaystyle{\displaylines{x_0 \in I}}$ و $\displaystyle{\displaylines{\forall x \in I \quad f(x) \leq f(x_0)}}$.
2) القيمة الدنيا :
نقول أن العدد $\displaystyle{\displaylines{f(x_0)}}$ هو القيمة الدنيا المطلقة للدالة $\displaystyle{\displaylines{f}}$ عند النقطة $\displaystyle{\displaylines{x_0}}$ إذا كان $\displaystyle{\displaylines{\forall x \in D_f \quad f(x) \geq f(x_0)}}$.
نقول أن العدد $\displaystyle{\displaylines{f(x_0)}}$ هو قيمة دنيا نسبية للدالة $\displaystyle{\displaylines{f}}$ عند النقطة $\displaystyle{\displaylines{x_0}}$ في المجال $\displaystyle{\displaylines{I}}$ إذا كان $\displaystyle{\displaylines{x_0 \in I}}$ و $\displaystyle{\displaylines{\forall x \in I \quad f(x) \geq f(x_0)}}$.
