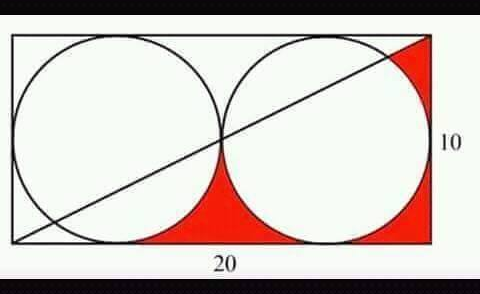
بالتناظر، المساحة المطلوبة هي مساحة الجزء الملون بالأحمر في الصورة التالية:
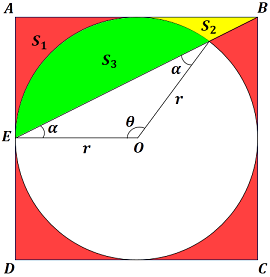$\displaystyle{\displaylines{AB=2r=10}}$لتكن
$\displaystyle{\displaylines{S}}$ مساحة الجزء الملون بالأحمر, لدينا :
$\displaystyle{\displaylines{S=S_q-S_c-S_2}}$حيث:
$\displaystyle{\displaylines{S_q}}$ مساحة المربع $\displaystyle{\displaylines{ABCD}}$
$\displaystyle{\displaylines{S_c}}$ مساحة الدائرة المرسومة داخل المربع
$\displaystyle{\displaylines{S_2}}$ مساحة الجزء الملون بالأصفر
لدينا:
$\displaystyle{\displaylines{S_q=10^2=100\quad,\quad S_c=\pi r^2=25\pi}}$$\displaystyle{\displaylines{S_2=S_t-S_1-S_3}}$حيث $\displaystyle{\displaylines{S_t}}$ هي مساحة المثلث $\displaystyle{\displaylines{ABE}}$ ($\displaystyle{\displaylines{S_1}}$ و $\displaystyle{\displaylines{S_3}}$ أنظر الشكل).
$\displaystyle{\displaylines{S_t=\frac{1}{4}S_q\quad,\quad S_1=\frac{1}{4}(S_q-S_c)}}$ومنه:
$\displaystyle{\displaylines{S_2=\frac{1}{4}S_q-\frac{1}{4}(S_q-S_c)-S_3=\frac{1}{4}S_c-S_3}}$بالتالي:
$\displaystyle{\displaylines{S=S_q-S_c-\frac{1}{4}S_c+S_3=S_q-\frac{5}{4}S_c+S_3}}$إذن:
$\displaystyle{\displaylines{S=100-\frac{125}{4}\pi+S_3}}$والآن بقي أن نحسب $\displaystyle{\displaylines{S_3}}$.
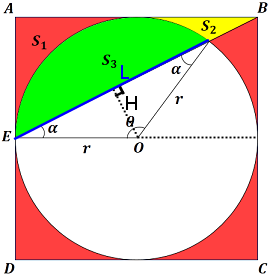باعتبار المثلث متساوي الساقين الذي رأسه $\displaystyle{\displaylines{O}}$, لدينا :
$\displaystyle{\displaylines{\theta=\pi-2\alpha}}$نعتبر $\displaystyle{\displaylines{S_{t1}}}$ مساحة هذا المثلث :
$\displaystyle{\displaylines{S_{t1} = \frac{H \times L}{2}}}$$\displaystyle{\displaylines{\sin(\alpha) = \frac{H}{r} \quad , \quad \cos(\alpha) = \frac{L}{2 r}}}$إذن
$\displaystyle{\displaylines{S_{t1} = r^2 \sin(\alpha) \cos(\alpha) = \frac{r^2}{2} \sin(2 \alpha)}}$وبما أن
$\displaystyle{\displaylines{\theta = \pi - 2 \alpha}}$, وكما هو معلوم :
$\displaystyle{\displaylines{\forall x \in \mathbb{R} \quad \sin(\pi - x) = \sin(x)}}$إذن :
$\displaystyle{\displaylines{\sin(\theta) = \sin(2 \alpha)}}$مساحة المثلث متساوي الساقين :
$\displaystyle{\displaylines{S_{t1} = \frac{r^2}{2} \sin(\theta)}}$بالنسبة للمساحة التي تكونها الزاوية
$\displaystyle{\displaylines{\theta}}$ في الدائرة فإنها تساوي
$\displaystyle{\displaylines{\frac{r^2}{2} \theta}}$.
إذن المساحة
$\displaystyle{\displaylines{S_3}}$ هي فرق هتين المساحتين, لدينا :
$\displaystyle{\displaylines{S_3=\frac{r^2}{2}(\theta-\sin\theta)}}$وبما أن $\displaystyle{\displaylines{\theta=\pi-2\alpha}}$ . لدينا:
$\displaystyle{\displaylines{\alpha=\arctan\frac{1}{2}\implies\theta=\pi-2\arctan\frac{1}{2}}}$ومنه:
$\displaystyle{\displaylines{\begin{align*}S_3 &=\frac{25}{2}\left(\pi-2\arctan\frac{1}{2}-\sin\Big(\pi-2\arctan\frac{1}{2}\Big)\right) \\[6pt]&=\frac{25}{2}\left(\pi-2\arctan\frac{1}{2}-\sin\Big(2\arctan\frac{1}{2}\Big)\right)\end{align*}}}$ولدينا:
$\displaystyle{\displaylines{\sin(\arctan x)=\frac{x}{\sqrt{1+x^2}} \quad , \quad \cos(\arctan x)=\frac{1}{\sqrt{1+x^2}}}}$ومنه:
$\displaystyle{\displaylines{\begin{align*}&\sin(2\arctan x)=2\sin(\arctan x)\cos(\arctan x)=\frac{2x}{1+x^2} \\[6pt]&\implies\sin\Big(2\arctan \frac{1}{2}\Big)=\frac{4}{5}\end{align*}}}$إذن:
$\displaystyle{\displaylines{\begin{align*}S_3&=\frac{25}{2}\left(\pi-2\arctan\frac{1}{2}-\frac{4}{5}\right)\\[6pt]&=\frac{25}{2}\pi-25\arctan\frac{1}{2}-10\end{align*}}}$وفي الأخير:
$\displaystyle{\displaylines{\begin{align*}S&=100-\frac{125}{4}\pi+\frac{25}{2}\pi-25\arctan\frac{1}{2}-10\\[6pt]&=90-\frac{75}{4}\pi-25\arctan\frac{1}{2}=19.5039...\end{align*}}}$
الرد على التعليق