بين المتساوية التالية

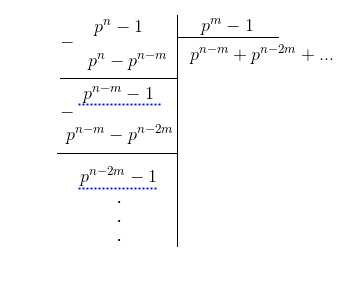
نقوم بانجاز القسمة الاقليدية للعدد $\displaystyle{\displaylines{a = p^n - 1}}$ على العدد $\displaystyle{\displaylines{b = p^m - 1}}$



لاحظ أن البواقي (المسطرة بالأزرق) تكتب على شكل $\displaystyle{\displaylines{p^{n - jm}-1}}$ بحيث $\displaystyle{\displaylines{j \in \mathbb{N}^{*}}}$

ليكن $\displaystyle{\displaylines{k}}$ بحيث $\displaystyle{\displaylines{p^{n - km}-1 < b}}$ هنا نكون قد أنجزنا القسمة الاقليدية للعدد $\displaystyle{\displaylines{a}}$ على $\displaystyle{\displaylines{b}}$

ولدينا $\displaystyle{\displaylines{0 \leq r = n-km < m}}$

خلاصة :

باقي القسمة الأقليدية للعدد $\displaystyle{\displaylines{a}}$ على $\displaystyle{\displaylines{b}}$ هو $\displaystyle{\displaylines{p^r - 1}}$ بحيث $\displaystyle{\displaylines{r = n - km}}$.

---

كما بينا في السؤال السابق لدينا :

باقي القسمة الأقليدية للعدد $\displaystyle{\displaylines{a}}$ على $\displaystyle{\displaylines{b}}$ هو $\displaystyle{\displaylines{p^r - 1}}$ بحيث $\displaystyle{\displaylines{r = n - km}}$.

لدينا :

$\displaystyle{\displaylines{\begin{array}{rcl}b | a & \iff & p^r - 1 = 0 \\& \iff & r = 0 \\& \iff & n = km \\& \iff & m | n\end{array}}}$

---

حسب مبرهنة Bézout لدينا :

$\displaystyle{\displaylines{d = n \wedge m \implies \exists (\alpha_1, \beta_1) \in \mathbb{Z}^{2} \ : \ d = \alpha_1 n + \beta_1 m}}$

إذن $\displaystyle{\displaylines{d = \alpha_1 n + k nm - k nm + \beta_1 m}}$

$\displaystyle{\displaylines{d = (\alpha_1 + km) n - (kn - \beta_1)m}}$

إذن يمكننا اختيار $\displaystyle{\displaylines{k \in \mathbb{Z}}}$ بحيث $\displaystyle{\displaylines{\alpha = \alpha_1 + km > 0}}$ و $\displaystyle{\displaylines{\beta = kn - \beta_1 > 0}}$

يعني يكفي أن تكون $\displaystyle{\displaylines{k > \frac{-\alpha_1}{m}}}$ و $\displaystyle{\displaylines{k > \frac{\beta_1}{n}}}$

نأخذ : $\displaystyle{\displaylines{k = \max \left( E\left( \frac{-\alpha_1}{m} \right) +1, E\left( \frac{\beta_1}{n} \right)+1 \right)}}$ بحيث $\displaystyle{\displaylines{E(x)}}$ دالة الجزء الصحيح

لدينا : $\displaystyle{\displaylines{d = \alpha n - \beta m}}$ بحيث $\displaystyle{\displaylines{\alpha > 0}}$ و $\displaystyle{\displaylines{\beta > 0}}$

---

لدينا : $\displaystyle{\displaylines{a=p^n-1}}$ و $\displaystyle{\displaylines{b=p^m-1}}$ بيحث $\displaystyle{\displaylines{n, m \in \mathbb{N}^{*}, \ n \geq m}}$

نضع : $\displaystyle{\displaylines{c = p^{n \wedge m} - 1}}$

لنبين أن $\displaystyle{\displaylines{a \wedge b = c}}$.

لدينا حسب السؤال الثاني :

$\displaystyle{\displaylines{\left\{ \begin{array}{cl}n \wedge m | n & \implies \ (p^{n \wedge m} - 1)|(p^n-1) \\n \wedge m | m & \implies \ (p^{n \wedge m} - 1)|(p^m-1)\end{array} \right.}}$

وبالتالي : $\displaystyle{\displaylines{c | a }}$ و $\displaystyle{\displaylines{c | b}}$

إذن :

$\displaystyle{\displaylines{c | a \wedge b \tag{1}}}$

الآن نضع $\displaystyle{\displaylines{d = n \wedge m}}$

حسب السؤال الثالث :

$\displaystyle{\displaylines{\exists (\alpha, \beta) \in \mathbb{N}^2 \, : \, \alpha n - \beta m = d}}$

لدينا $\displaystyle{\displaylines{a \wedge b | a}}$ و أيضا $\displaystyle{\displaylines{a = p^n - 1 | p^{\alpha n} - 1}}$ لأن $\displaystyle{\displaylines{n | \alpha n}}$

إذن $\displaystyle{\displaylines{a \wedge b | p^{\alpha n} - 1}}$

لدينا $\displaystyle{\displaylines{a \wedge b | b}}$ وايضا $\displaystyle{\displaylines{b = p^m - 1 | p^{\beta m} - 1}}$ لأن $\displaystyle{\displaylines{m | \beta m}}$

إذن $\displaystyle{\displaylines{a \wedge b | p^{\beta m} - 1}}$.

خلاصة :



إذن $\displaystyle{\displaylines{a \wedge b | p^{\beta m} (p^{\alpha n - \beta m} - 1)}}$

لاحظ أن $\displaystyle{\displaylines{a \wedge p = b \wedge p = 1}}$ وبالتالي $\displaystyle{\displaylines{(a \wedge b) \wedge p = 1}}$

إذن $\displaystyle{\displaylines{(a \wedge b) \wedge p^{\beta m} = 1}}$

إذن حسب مبرهنة Gauss لدينا : $\displaystyle{\displaylines{a \wedge b | p^{\alpha n - \beta m} - 1 = p^d - 1}}$

إذن :

$\displaystyle{\displaylines{a \wedge b | c \tag{2}}}$

من $\displaystyle{\displaylines{(1)}}$ و $\displaystyle{\displaylines{(2)}}$ لدينا : $\displaystyle{\displaylines{a \wedge b = c}}$