يُعتبر العدد
$\displaystyle{\displaylines{\pi}}$ أشهر الثوابت الرياضية وأهمها على الإطلاق, فلا يوجد اليوم فرع من فروع الرياضيات إلا ونجد هذا العدد مرتبطا به.
شُهرة العدد
$\displaystyle{\displaylines{\pi}}$ وانتشاره داخل مختلف المجالات قاد لانتشار بعض المعلومات الخاطئة والمغلوطة عن طبيعته مثل أننا لا نعلم الرقم الأخير في كتابته العشرية أو أن العلماء لا يعلمون هل أرقامه بعد الفاصلة تنتهي أم لا, وفي هذا الموضوع سنحاول إزالة أي لُبس حول طبيعة هذا العدد.
تعريف العدد π
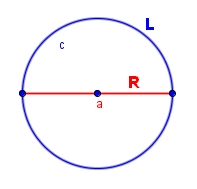
دائرة.
اللون الأحمر يمثل قطر الدائرة R.
اللون الأزرق يمثل محيط الدائرة L.
يُمكننا تعريف العدد
$\displaystyle{\displaylines{\pi}}$ على أنه
محيط الدائرة نسبة إلى قطرها أي أن :
$\displaystyle{\displaylines{\begin{array}{rcl}\pi & = & \dfrac{{\color{Blue} L}}{{\color{Red} R}} \\ \\& = & 3.14159265359 \cdots \\\end{array}}}$
وهذه النسبة هي ثابتة كيفما كانت الدائرة.
كان العدد
$\displaystyle{\displaylines{\pi}}$ معروفا في العديد من الحضارات القديمة مثل البابليين والفراعنة و الحضارات الصينية القديمة بسبب ارتباط هذا العدد بالإنشاءات العمرانية, لكن قيمته الرقمية المستخدمة آنذاك كانت دقتها ضعيفة..
ويعتبر أرخميدس (300 سنة قبل الميلاد) أول من استطاع تأطير قيمة العدد
$\displaystyle{\displaylines{\pi}}$ بشكل صحيح عبر تقريبه للدائرة بمضلعين منتظمين مكونين من 96 ضلع, أحدهما داخل الدائرة والآخر خارجها.
هكذا استطاع أرخميدس إثبات النتيجة :
$\displaystyle{\displaylines{\cdots 3,14084 = \frac{223}{71}< \pi < \frac{22}{7}=3,14285\cdots}}$
باستخدام طريقة أرخميدس استطاع كل من الخوارزمي والكاشي من زيادة دقة حساب العدد
$\displaystyle{\displaylines{\pi}}$ حيث استطاع الكاشي سنة 1424 من حساب
$\displaystyle{\displaylines{16}}$ رقم بعد الفاصلة .
وقد تطورت أساليب حساب العدد
$\displaystyle{\displaylines{\pi}}$ بتطور حساب التفاضل والتكامل في القرن 17 على يد كل من ليبنيز وإسحق نيوتن.
وقد قاد هذا التطور إلى طرح التساؤل حول طبيعة العدد $\displaystyle{\displaylines{\pi}}$ هل هو جذري أو لاجذري ؟سنة 1761 سوف يتمكن Lambert من إثبات أن العدد
$\displaystyle{\displaylines{\pi}}$ عدد لاجذري (
nombre irrationnel), أي أنه لا يمكن كتابته على شكل
$\displaystyle{\displaylines{\frac{a}{b}}}$ بحيث
$\displaystyle{\displaylines{a}}$ و
$\displaystyle{\displaylines{b}}$ أعداد صحيحة طبيعية.
وقد ارتبط العدد
$\displaystyle{\displaylines{\pi}}$ أيضا بواحدة من أقدم المسائل المفتوحة في الهندسة, وهي مسألة تربيع الدائرة. وتبحث هذه المسألة على طريقة رسم مربع له نفس مساحة دائرة عن طريق المسطرة والبركار فقط !
وقد قاد تطور الهندسة التحليلية في القرن 17 الذي حول الدوائر والمستقيمات إلى دوال, وتقاطعها إلى معادلات معاملاتها أعداد جذرية إلى اختزال مراحل استعمال المسطرة والبركار إلى معادلات.
سنة 1882 تمكن Lindemann من حل معضلة تربيع الدائرة عبر إثباته أن
$\displaystyle{\displaylines{\pi}}$ عدد متسامي transcendant أي ليس حلا لأية معادلة معاملاتها في
$\displaystyle{\displaylines{\mathbb{Q}}}$ وبالتالي استحالة إنشاء مربع له نفس مساحة الدائرة باستعمال المسطرة والبركار فقط .
تعريف العدد الجذري
نقول عن عدد
$\displaystyle{\displaylines{x}}$ أنه جذري (
nombre rationel) إذا وفقط إذا كان
$\displaystyle{\displaylines{x = \frac{p}{q}}}$ بحيث
$\displaystyle{\displaylines{p}}$ و
$\displaystyle{\displaylines{q}}$ أعداد صحيحة نسبية.
أمثلة : $\displaystyle{\displaylines{\frac{5}{11},\, \frac{8}{23},\,-\frac{1}{4}}}$وبصفة عامة نعرف مجموعة الأعداد الجذرية كالتالي :
$\displaystyle{\displaylines{ \mathbb{Q} = \left\{ \frac{n}{m} \, \middle | \, (n,m) \in \mathbb{Z} \times \mathbb{N}^{*} \right\}}}$
ويمكننا إثبات أن عددا
$\displaystyle{\displaylines{r}}$ جذري إذا وفقط إذا كانت أرقامه بعد الفاصلة منتهية أو دورية.
سلسلة الأرقام بعد الفاصلة منتهية أو دورية $\displaystyle{\displaylines{ r \in \mathbb{Q} \iff}}$
أمثلة :$\displaystyle{\displaylines{\begin{array}{rcl}\dfrac{1}{2} & = & 0.5 \\\dfrac{1}{3} & = & 0.33333\cdots \\\dfrac{16}{13} & = & 1.{\color{Red} 2}30769{\color{Red} 2}30769{\color{Red} 2}30\cdots \\\dfrac{45}{32} & = & 1.40625\end{array}}}$
تعريف العدد اللاجذري
نُعرف مجموعة الأعداد اللاجذرية بالأعداد الحقيقية التي لا تنتمي إلى
$\displaystyle{\displaylines{\mathbb{Q}}}$ :
$\displaystyle{\displaylines{\mathbb{R} \smallsetminus \mathbb{Q}}}$
انطلاقا من تعريف الأعداد الجذرية يمكننا استنتاج أن الأعداد اللاجذرية لا يمكن أن تكون أرقامها بعد الفاصلة منتهية أو دورية.
أمثلة لأعداد تم إثبات أنها لاجذرية :$\displaystyle{\displaylines{\begin{array}{rcl}\ln(2) & = & 0.693147180 \cdots \\e & = & 2.718281828 \cdots \\\sqrt{3} & = & 1.732050807 \cdots\end{array}}}$
تصحيح المغالطة
"لا نعلم هل الأرقام بعد الفاصلة للعدد
$\displaystyle{\displaylines{\pi}}$ تنتهي أم لا" : هذه المقولة التي لطالما سمعناها في القسم وفي الدروس هي خاطئة لأننا كما رأينا سابقا أن العدد
$\displaystyle{\displaylines{\pi}}$ عدد لاجذري وإن وُجد رقم هو الأخير في سلسلة الأرقام بعد الفاصلة لهذا العدد فسيصبح عددا جذريا وهذا تناقض !
وهذه بعض المعلومات عن العدد
$\displaystyle{\displaylines{\pi}}$ :
- لا يمكن للأرقام بعد الفاصلة للعدد $\displaystyle{\displaylines{\pi}}$ أن تكون منتهية أو دورية.
- بما أن العدد $\displaystyle{\displaylines{\pi}}$ لاجذري, فإنه يمكن إيجاد أي سلسلة رقمية في أرقامه بعد الفاصلة.
- العدد $\displaystyle{\displaylines{\pi}}$ متسامي transcendant, فلا يمكنه أن يكون حلا لمعادلة حدودية معاملاتها في $\displaystyle{\displaylines{\mathbb{Q}}}$.
السؤال الذي يطرح نفسه لماذا يبحث العلماء عن أرقام بعد الفاصلة تصل للملايير؟هذا سؤال وجيه, لأن العلماء يحسبون الأرقام بعد الفاصلة ليكتشفوا ربما عن طريق التجربة علاقة محتملة قد تربط بين
$\displaystyle{\displaylines{\pi}}$ وأعداد أخرى مثل
$\displaystyle{\displaylines{e}}$ أو ثابتة أويلر
$\displaystyle{\displaylines{\gamma}}$.
أو تنسيق رياضي سهل يمكن أن نحسب بواسطته العدد
$\displaystyle{\displaylines{\pi}}$ .
وهناك من يحسب هذه الأرقام فقط لتحقيق السبق حيث التنافس عن من حقق أكبر رقم بعد الفاصلة, ولتحقيق ذلك يبحث العلماء عن متسلسلات (
séries)
سريعة التقارب لحساب العدد
$\displaystyle{\displaylines{\pi}}$. مثل الصيغة التي وجدها
David و
Gregory Chudnovsky, والتي تعطي 14 رقم فاصلة صحيح جديد في كل تصاعد لـ
$\displaystyle{\displaylines{k}}$ :
$\displaystyle{\displaylines{\frac{426880 \sqrt{10005}}{\pi} = \sum_{k=0}^{+ \infty} \frac{(6k)! (13591409 + 545140134k)}{(3k)! (k!)^3(-640320)^{3k}}}}$
