نعرف دالة الجزء الصحيح لمتغير حقيقي
$\displaystyle{\displaylines{x}}$ على أنها أكبر عدد صحيح نسبي
$\displaystyle{\displaylines{n}}$ يحقق
$\displaystyle{\displaylines{n \leq x}}$ :
$\displaystyle{\displaylines{\text{E} :\begin{array}{rcl}\mathbb{R} & \rightarrow & \mathbb{Z} \\x & \rightarrow & \text{E}(x) = \max\{n \in \mathbb{Z} \, | \, n \leq x\} \end{array}}}$
ترميز : نرمز لدالة الجزء الصحيح بـ
$\displaystyle{\displaylines{\text{E}(x)}}$ أو
$\displaystyle{\displaylines{\text{floor}(x)}}$ أو
$\displaystyle{\displaylines{[x]}}$ أو
$\displaystyle{\displaylines{\lfloor x \rfloor}}$.
وفي كل ما سيأتي سوف نستخدم
$\displaystyle{\displaylines{\text{E}(x)}}$ لتمثيل الجزء الصحيح للعدد
$\displaystyle{\displaylines{x}}$.
خصائص : ليكن
$\displaystyle{\displaylines{x \in \mathbb{R}}}$ انطلاقا من تعريف دالة الجزء الصحيح, لدينا :
$\displaystyle{\displaylines{\begin{array}{rcl}\text{E}(x) = n & \iff & n \leq x < n + 1 \\ \\& \iff & x - 1 < n \leq x \end{array}}}$
أو بصيغة أخرى لدينا :
$\displaystyle{\displaylines{\begin{array}{rcl}\forall x \in \mathbb{R} & : & x - 1 < \text{E}(x) \leq x \\ \\& : & \text{E}(x) \leq x < \text{E}(x) + 1 \end{array}}}$
أمثلة :- $\displaystyle{\displaylines{\text{E}(5.36) = 5}}$
- $\displaystyle{\displaylines{\text{E}(1.999) = 1 }}$
- $\displaystyle{\displaylines{\text{E}(-3) = -3}}$
- $\displaystyle{\displaylines{\text{E}(-3.14) = -4}}$
ليكن
$\displaystyle{\displaylines{n, m \in \mathbb{Z}}}$ و
$\displaystyle{\displaylines{x}}$ عدد حقيقي, لدينا :
$\displaystyle{\displaylines{\begin{array}{rcl}n < x & \implies & n \leq \text{E}(x) \\ \\x < m & \implies & \text{E}(x) < m \end{array}}}$
وبالتالي فإنه وإذا كان
$\displaystyle{\displaylines{x \in ]n,m[}}$ بحيث
$\displaystyle{\displaylines{n}}$ و
$\displaystyle{\displaylines{m}}$ أعداد صحيحة نسبية فإن
$\displaystyle{\displaylines{\text{E}(x) \in \{n,n+1,\cdots,m-1\}}}$.
ملاحظة : يجب الحذر مع أطراف المجالات في التعامل مع دالة الجزء الصحيح, ويجب دائما استحظار التعريف أن
$\displaystyle{\displaylines{\text{E}(x)}}$ تمثل أكبر عدد صحيح نسبي يحقق
$\displaystyle{\displaylines{\text{E}(x)=n \leq x}}$.
تمرين 1 : بين الخاصيات التالية :
$\displaystyle{\displaylines{(\forall x \in \mathbb{R}) \, (\forall n \in \mathbb{Z}) \, : \quad \text{E}(x + n) = n + \text{E}(x)}}$
$\displaystyle{\displaylines{(\forall x,y \in \mathbb{R}) \, : \quad \text{E}(x) + \text{E}(y) \leq \text{E}(x + y) \leq \text{E}(x) + \text{E}(y) + 1}}$
$\displaystyle{\displaylines{(\forall x \in \mathbb{R}) \, (\forall n \in \mathbb{N}^{*}) \, : \quad 0 \leq \text{E}(n x) - n \text{E}(x) \leq n - 1}}$
تصحيح التمرين :
تمرين حول دالة الجزء الصحيح.
تمرين 2 : ليكن
$\displaystyle{\displaylines{a,b \in \mathbb{N}^{*}}}$.
نقوم بالقسمة الأقليدية للعدد
$\displaystyle{\displaylines{a}}$ على
$\displaystyle{\displaylines{b}}$ :
$\displaystyle{\displaylines{a = bq + r \, , \quad 0 \leq r < b}}$, بين أن :
$\displaystyle{\displaylines{q = \text{E}\left( \frac{a}{b} \right)}}$بين أن :
$\displaystyle{\displaylines{\forall n,p,q \in \mathbb{N}^{*} \, : \quad \text{E}\left( \frac{\text{E}\left( \frac{n}{p} \right)}{q} \right) = \text{E}\left( \frac{n}{p q} \right)}}$تصحيح التمرين :
بين المتساويتين.
دراسة الدالة f(x) = E(x) :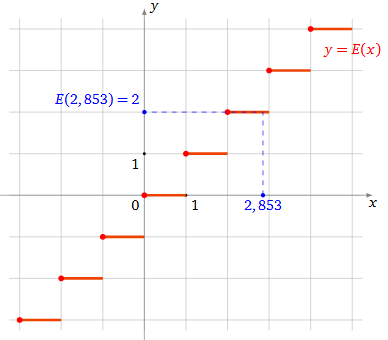
رسم دالة الجزء الصحيح
ليكن
$\displaystyle{\displaylines{x, y \in \mathbb{R}}}$ بحيث
$\displaystyle{\displaylines{x \leq y}}$.
نعتبر المجموعتين
$\displaystyle{\displaylines{A_x = \{ n \in \mathbb{Z} \, | \, n \leq x \} \quad A_y = \{ n \in \mathbb{Z} \, | \, n \leq y \}}}$لدينا
$\displaystyle{\displaylines{x \leq y \implies A_x \subset A_y}}$إذن
$\displaystyle{\displaylines{\max A_x \leq \max A_y}}$إذن
$\displaystyle{\displaylines{\text{E}(x) \leq \text{E}(y)}}$وبالتالي فإن الدالة
$\displaystyle{\displaylines{E}}$ تزايدية على
$\displaystyle{\displaylines{\mathbb{R}}}$الدالة E غير متصلة من أجل $\displaystyle{\displaylines{\color{DarkRed} n \in \mathbb{Z}}}$ : لدينا
$\displaystyle{\displaylines{\mathbb{R} = \bigcup_{n \in \mathbb{Z}} [n, n+1[}}$وبالتالي
$\displaystyle{\displaylines{\forall x \in \mathbb{R} \, , \, x \in [n,n+1[ \, : \quad \text{E}(x) = n}}$لدينا
$\displaystyle{\displaylines{\lim_{\substack{ x \rightarrow n \\ x > n }} \text{E}(x) = \lim_{\substack{ x \rightarrow n \\ x > n }} n = n}}$ولدينا
$\displaystyle{\displaylines{\forall x \in [n-1,n[ \, : \quad \text{E}(x) = n-1}}$وبالتالي
$\displaystyle{\displaylines{\lim_{\substack{ x \rightarrow n \\ x < n }} \text{E}(x) = \lim_{\substack{ x \rightarrow n \\ x < n }} n-1 = n-1}}$لاحظ أن النهاية على اليمين تخالف النهاية على اليسار وبالتالي فإن الدالة
$\displaystyle{\displaylines{\text{E}}}$ غير متصلة في النقطة
$\displaystyle{\displaylines{n}}$. إذن
$\displaystyle{\displaylines{E}}$ ليست متصلة من أجل
$\displaystyle{\displaylines{x \in \mathbb{Z}}}$.
الدالة E متصلة على يمين كل نقطة a من IR:لدينا
$\displaystyle{\displaylines{\forall x \in \mathbb{R} \, , \, x \in [n,n+1[ \, : \quad \text{E}(x) = n}}$ليكن
$\displaystyle{\displaylines{a \in [n,n+1[}}$ :
إذا كان
$\displaystyle{\displaylines{a \in \mathbb{Z}}}$ فإن
$\displaystyle{\displaylines{a=n}}$ وكما بينا سابقا
$\displaystyle{\displaylines{\lim_{\substack{ x \rightarrow a \\ x > a }} \text{E}(x) = \lim_{\substack{ x \rightarrow a \\ x > a }} a = a = \text{E}(a)}}$إذا كان
$\displaystyle{\displaylines{a \notin \mathbb{Z}}}$ لدينا
$\displaystyle{\displaylines{\lim_{\substack{ x \rightarrow a \\ x > a }} \text{E}(x) = \lim_{\substack{ x \rightarrow a \\ x > a }} n = n = \text{E}(a)}}$وبالتالي فإن الدالة E متصلة على يمين كل نقطة x من
$\displaystyle{\displaylines{\mathbb{R}}}$