ليكن
$\displaystyle{\displaylines{n \in \mathbb{N}^{*}}}$, بين أن :
$\displaystyle{\displaylines{\forall x \in ]0, + \infty[ \ : \ n (1 - x^{-\frac{1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}}-1)}}$استنتج أن
$\displaystyle{\displaylines{\forall x \in ]0, + \infty[}}$ :
$\displaystyle{\displaylines{\lim_{n \to +\infty}n (x^{\frac{1}{n}}-1) = \lim_{n \to +\infty} n (1 - x^{-\frac{1}{n}}) = \ln(x)}}$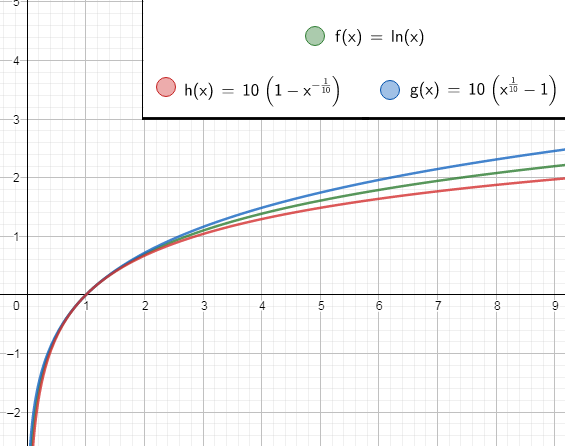
مثال من أجل n=10.
لدينا :
$\displaystyle{\displaylines{\forall n \in \mathbb{N^{*}} \, : \, -1-\frac{1}{n} \leq -1 \leq -1 + \frac{1}{n}}}$
* إذا كان $\displaystyle{\displaylines{x \geq 1}}$ :
لدينا :
$\displaystyle{\displaylines{( \forall n \in \mathbb{N^{*}} ) \, ( \forall t \geq 1 ) \, : \, t^{-1-\frac{1}{n}} \leq t^{-1} \leq t^{-1 + \frac{1}{n}}}}$
$\displaystyle{\displaylines{\int_{1}^{x} t^{-1-\frac{1}{n}} dt \leq \int_{1}^{x} t^{-1} dt \leq \int_{1}^{x} t^{-1 + \frac{1}{n}} dt}}$
و بالتالي :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in [1, +\infty[) \ : \ n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
* إذا كان $\displaystyle{\displaylines{x \in ]0, 1]}}$ :
لدينا :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in [1, +\infty[) \ : \ n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
نضع : $\displaystyle{\displaylines{t = \frac{1}{x}}}$, لدينا إذن : $\displaystyle{\displaylines{ t \geq 1 }}$.
إذن :
$\displaystyle{\displaylines{n (1-t^{\frac{-1}{n}}) \leq \ln(t) \leq n (t^{\frac{1}{n}} - 1)}}$
وبالتالي:
$\displaystyle{\displaylines{n (1-x^{\frac{1}{n}}) \leq \ln\left( \frac{1}{x} \right) \leq n (x^{-\frac{1}{n}} - 1)}}$
إذن :
$\displaystyle{\displaylines{n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
وبالتالي :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in ]0, 1]) \ : \ n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
نتيجة :
$\displaystyle{\displaylines{\color{DarkRed} (\forall n \in \mathbb{N}^{*}) \ (\forall x \in ]0, +\infty[) \ : \ n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
بينا في السؤال السابق :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in ]0, +\infty[) \ : \ n (1-x^{\frac{-1}{n}}) \leq \ln(x) \leq n (x^{\frac{1}{n}} - 1)}}$
وبالتالي :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in ]0, +\infty[) \ : \ \ln(x) \leq n (x^{\frac{1}{n}}-1) \leq x^{\frac{1}{n}} \ln(x) \tag{1}}}$
وأيضا :
$\displaystyle{\displaylines{(\forall n \in \mathbb{N}^{*}) \ (\forall x \in ]0, +\infty[) \ : \ x^{\frac{-1}{n}} \ln(x) \leq n (1 - x^{-\frac{1}{n}}) \leq \ln(x) \tag{2}}}$
من خلال $\displaystyle{\displaylines{(1)}}$ و $\displaystyle{\displaylines{(2)}}$ لدينا $\displaystyle{\displaylines{\forall x \in ]0, + \infty [}}$ :
$\displaystyle{\displaylines{\lim_{n \rightarrow + \infty} x^{\frac{1}{n}} \ln(x) = \lim_{n \rightarrow + \infty} x^{\frac{-1}{n}} \ln(x) = \ln(x)}}$
إذن :
$\displaystyle{\displaylines{\color{DarkRed} \lim_{n \to +\infty}n (x^{\frac{1}{n}}-1) = \lim_{n \to +\infty} n (1 - x^{-\frac{1}{n}}) = \ln(x)}}$
