لتكن الدالة $\displaystyle{\displaylines{f}}$ المعرفة بـ:
$\displaystyle{\displaylines{f(x)=2\sqrt{x}-\ln(x)}}$1) أدرس تغيرات الدالة $\displaystyle{\displaylines{f}}$ واستنتج إشارتها.
2) بين أن:
$\displaystyle{\displaylines{\forall x > 1 \ : \ 0 < \frac{\ln(x)}{x} < \frac{2}{\sqrt{x}}}}$3) استنتج أن:
$\displaystyle{\displaylines{\lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}=0}}$ 1) أولا: مجموعة التعريف
الدالة $\displaystyle{\displaylines{x \to \sqrt{x}}}$ معرفة على المجال $\displaystyle{\displaylines{[0,+\infty[}}$
والدالة $\displaystyle{\displaylines{x \to \ln(x)}}$ معرفة على المجال $\displaystyle{\displaylines{]0,+\infty[}}$
ومنه مجموعة تعريف الدالة $\displaystyle{\displaylines{x \to f(x)}}$ هي $\displaystyle{\displaylines{]0,+\infty[}}$.
ثانيا: الدالة المشتقة
الدالة $\displaystyle{\displaylines{x \to \sqrt{x}}}$ قابلة للإشتقاق على المجال $\displaystyle{\displaylines{]0,+\infty[}}$
والدالة $\displaystyle{\displaylines{x \to \ln(x)}}$ قابلة للإشتقاق على المجال $\displaystyle{\displaylines{]0,+\infty[}}$
ومنه فإن الدالة $\displaystyle{\displaylines{x \to f(x)}}$ قابلة للإشتقاق على $\displaystyle{\displaylines{]0,+\infty[}}$, ولدينا :
$\displaystyle{\displaylines{ \begin{align*}\forall x \in ]0, +\infty[ \ : \ f^{'}(x) & = 2(\sqrt{x})'-(\ln(x))' \\& = 2\frac{1}{2\sqrt{x}}-\frac{1}{x} \\& = \frac{1}{\sqrt{x}}-\frac{1}{x} \\& = \frac{\sqrt{x}-1}{x}\end{align*} }}$
ثالثا: إشارة الدالة المشتقة
$\displaystyle{\displaylines{ \begin{align*}f'(x)=0 & \iff\sqrt{x}-1=0 \\& \iff \sqrt{x}=1 \\& \iff x=1\end{align*} }}$ ومنه الدالة المشتقة تنعدم عند $\displaystyle{\displaylines{x=1}}$
المقام موجب لأن $\displaystyle{\displaylines{x>0}}$ ومنه إشارة $\displaystyle{\displaylines{f'}}$ من إشارة البسط.
$\displaystyle{\displaylines{ \begin{align*}f'(x)>0 & \iff\sqrt{x}-1>0 \\& \iff \sqrt{x}>1 \\& \iff x>1\end{align*} }}$وأخيرا، جدول تغيرات الدالة
$\displaystyle{\displaylines{f}}$ هو
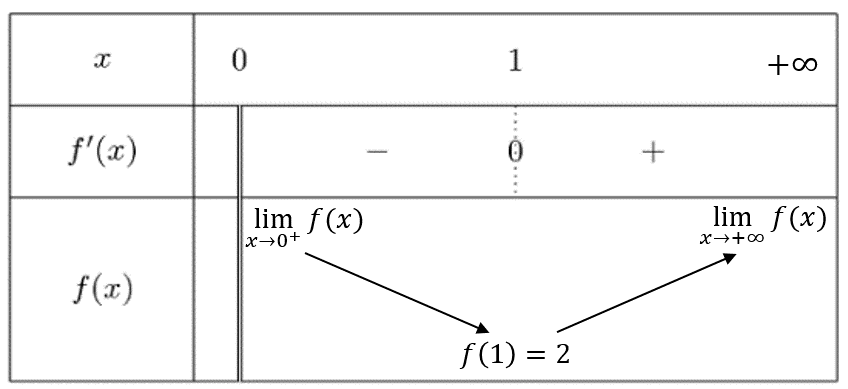
ومن جدول التغيرات نلاحظ أن الدالة $\displaystyle{\displaylines{f}}$ موجبة على مجموعة تعريفها.
2) لدينا من جهة
$\displaystyle{\displaylines{ x>1 \implies \ln(x)>0 \implies \frac{\ln(x)}{x}>0 }}$ لدينا من خلال جدول التغيرات :
$\displaystyle{\displaylines{\forall x > 1 \ : \ f^{'}(x)>0}}$وبالتالي فإن الدالة $\displaystyle{\displaylines{f}}$ تزايدية قطعا على المجال $\displaystyle{\displaylines{[1, +\infty[}}$, لدينا :
$\displaystyle{\displaylines{\begin{align*}\forall x>1:f(x) > f(1)=2>0 & \iff 2\sqrt{x}-\ln(x)>0 \\& \iff \ln(x) < 2\sqrt{x} \\& \iff \dfrac{\ln(x)}{x} < \dfrac{2}{\sqrt{x}}\end{align*}}}$ ومنه:
$\displaystyle{\displaylines{ \forall x>1:0<\frac{\ln(x)}{x}<\frac{2}{\sqrt{x}} }}$
3) بإدخال النهاية على النتيجة الأخيرة نجد
$\displaystyle{\displaylines{ \lim_{x\rightarrow +\infty} 0 \leqslant \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x} \leqslant \lim_{x\rightarrow +\infty} \frac{2}{\sqrt{x}} }}$$\displaystyle{\displaylines{\begin{align*} & \implies 0 \leqslant \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x} \leqslant 0 \\& \implies \lim_{x\to +\infty} \frac{\ln(x)}{x} = 0 \end{align*}}}$