لتكن
$\displaystyle{\displaylines{f}}$ دالة متصلة على مجال
$\displaystyle{\displaylines{[a, b]}}$ بحيث :
$\displaystyle{\displaylines{\lim_{x \rightarrow a^{+} } \frac{f(x)-f(a)}{x-a} = l \in \mathbb{R}}}$
1) بين أن : $\displaystyle{\displaylines{(\exists k \geq 0) \, (\forall x \in [a, b]) \, : \, |f(x) - f(a)| \leq k |x-a|}}$
2) تطبيق : نضع $\displaystyle{\displaylines{ \forall x \in [0, 1] \, : \, f(x) = \arctan(x)}}$
بين أنه : $\displaystyle{\displaylines{(\exists k > 0) \, (\forall x \in [0, 1]) \, : \, \arctan(x) \leq k x}}$
ثم استنتج أن : $\displaystyle{\displaylines{ 1 \leq k }}$ .
3) نضع $\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ f(x) = \tan(x)}}$ ونفترض أن :
$\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ f(x) \neq x^3 + x}}$
بين أن $\displaystyle{\displaylines{ \forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ x < \tan(x) < x^3 + x}}$
4) إستنتج أن : $\displaystyle{\displaylines{\lim_{x \rightarrow 0 } \frac{\arctan(x) - x}{x^2} = 0}}$
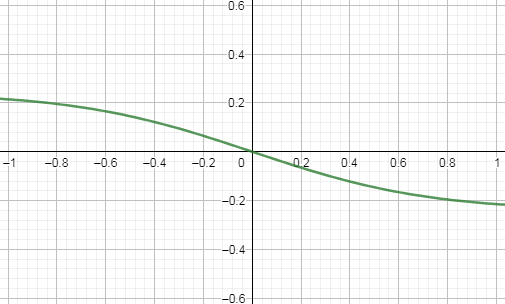
رسم الدالة $\displaystyle{\displaylines{\tiny\frac{\arctan(x) - x}{x^2}}}$ في المجال $\displaystyle{\displaylines{\tiny[-1, 1]}}$
تذكير :
إذا كانت $\displaystyle{\displaylines{f}}$ دالة متصلة على $\displaystyle{\displaylines{[a, b]}}$ فإنه :
$\displaystyle{\displaylines{(\exists k \geq 0) \, (\forall x \in [a, b]) \, : \, |f(x)| \leq k}}$
إذا وضعنا :
$\displaystyle{\displaylines{g(x)=\left\{\begin{matrix}\frac{f(x)-f(a)}{x-a} \, , x \in ]a, b] \\ \\l \, , x = a\end{matrix}\right.}}$
لدينا $\displaystyle{\displaylines{g}}$ دالة متصلة على $\displaystyle{\displaylines{[a, b]}}$ لأن $\displaystyle{\displaylines{g}}$ متصلة على $\displaystyle{\displaylines{]a, b]}}$ و $\displaystyle{\displaylines{ \lim_{x \rightarrow a^{+} } g(x) = g(a) = l}}$
و بالتالي : $\displaystyle{\displaylines{(\exists k \geq 0) \, (\forall x \in [a, b]) \, : \, |g(x)| \leq k}}$
إذن :
$\displaystyle{\displaylines{\color{DarkRed}(\exists k \geq 0) \, (\forall x \in [a, b]) \, : \, |f(x) - f(a)| \leq k |x-a|}}$
يكفي التطبيق على السؤال 1 , لدينا :
الدالة $\displaystyle{\displaylines{\arctan}}$ متصلة على $\displaystyle{\displaylines{[0, 1] }}$ و أيضا :
$\displaystyle{\displaylines{\lim_{x \rightarrow 0^{+} } \frac{\arctan(x)}{x} = \arctan^{'}(0) = 1 \in \mathbb{R}}}$
لاحظ أن( $\displaystyle{\displaylines{\forall x \in \mathbb{R} \, : \, \arctan^{'}(x) = \frac{1}{x^2 + 1} }}$ )
إذن :
$\displaystyle{\displaylines{\color{DarkRed}(\exists k > 0) \, (\forall x \in [0, 1]) \, : \, \arctan(x) \leq k x}}$
وبالتالي : $\displaystyle{\displaylines{ \forall x \in ]0, 1] \, : \, \frac{\arctan(x)}{x} \leq k }}$ .
إذن :
$\displaystyle{\displaylines{\lim_{x\rightarrow 0^+} \frac{\arctan(x)}{x} \leq k}}$
إذن
$\displaystyle{\displaylines{\color{DarkRed}1 \leq k}}$
لنبين أن : $\displaystyle{\displaylines{ \forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ \tan(x) < x^3 + x }}$
نضع $\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ h(x) = x^3 + x - \tan(x)}}$
لدينا $\displaystyle{\displaylines{h}}$ متصلة على $\displaystyle{\displaylines{\left]0, \frac{\pi}{4}\right[}}$
لدينا حسب السؤال : $\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ \tan(x) \neq x^3 + x}}$
إذن : $\displaystyle{\displaylines{ \forall x \in \left]0, \frac{\pi}{4}\right[ \, : \, h(x) \neq 0}}$
إذن فالدالة $\displaystyle{\displaylines{h}}$ تحافظ على إشارة تابثة في المجال $\displaystyle{\displaylines{\left]0, \frac{\pi}{4}\right[}}$
(لأنه إذا وجد $\displaystyle{\displaylines{\alpha}}$ و $\displaystyle{\displaylines{\beta}}$ من $\displaystyle{\displaylines{\left]0, \frac{\pi}{4}\right[}}$ بحيث $\displaystyle{\displaylines{h(\alpha)}}$ و $\displaystyle{\displaylines{h(\beta)}}$ لهما إشارتان مختلفتان فإنه حسب
مبرهنة القيم الوسطية : $\displaystyle{\displaylines{\exists c \in [\alpha, \beta] \subset ]0, \frac{\pi}{4}[ \, : \, h(c) = 0 }}$.تناقض !)
ولدينا : $\displaystyle{\displaylines{\frac{\pi}{6} \in \left]0, \frac{\pi}{4}\right[ }}$ و $\displaystyle{\displaylines{h\left(\frac{\pi}{6}\right) > 0}}$. إذن :
$\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ h(x) \gt 0}}$
إذن :
$\displaystyle{\displaylines{\color{DarkRed}\forall x \in \left]0, \frac{\pi}{4}\right[ \, : \, \tan(x) < x^3 + x}}$
لنبين أن : $\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ x < \tan(x)}}$
نضع $\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ g(x) = \tan(x) - x}}$
لدينا $\displaystyle{\displaylines{g}}$ قابلة للإشتقاق على $\displaystyle{\displaylines{\left]0, \frac{\pi}{4}\right[}}$ و لدينا :
$\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ g^{'}(x) = \tan^{2}(x) > 0}}$
لدينا $\displaystyle{\displaylines{g}}$ تزايدية قطعا على $\displaystyle{\displaylines{\left]0, \frac{\pi}{4}\right[}}$ و متصلة على $\displaystyle{\displaylines{\left[0, \frac{\pi}{4}\right[}}$
وبالتالي :
$\displaystyle{\displaylines{\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ g(0)=0 < g(x)}}$
إذن :
$\displaystyle{\displaylines{\color{DarkRed}\forall x \in \left]0, \frac{\pi}{4}\right[ \ : \ x < \tan(x)}}$
لنحدد النهاية التالية : $\displaystyle{\displaylines{\lim_{x \rightarrow 0 } \frac{\arctan(x) - x}{x^2}}}$
سوف نقوم بحساب النهاية في وقت أول على يمين $\displaystyle{\displaylines{0}}$, ثم نستنتج النهاية على يسار الصفر باعتبار أن الدالة $\displaystyle{\displaylines{x \rightarrow \frac{\arctan(x) - x}{x^2}}}$ فردية
نضع $\displaystyle{\displaylines{x = \tan(a)}}$
لدينا $\displaystyle{\displaylines{ x \rightarrow 0^+ \iff a \rightarrow 0^+ }}$
لدينا :
$\displaystyle{\displaylines{\begin{array}{rcl}\displaystyle\lim_{x \rightarrow 0^+ } \dfrac{\arctan(x) - x}{x^2} & = & \displaystyle\lim_{a \rightarrow 0^+ } \dfrac{a - \tan(a)}{\tan^2(a)} \\ \\ \\~ & = & \displaystyle\lim_{a \rightarrow 0^+ } \dfrac{a - \tan(a)}{a^2 \dfrac{\tan^2(a)}{a^2}}\end{array}}}$
لدينا حسب ما سبق :
$\displaystyle{\displaylines{\forall a \in \left]0, \frac{\pi}{4}\right[ \ : \ a < \tan(a) < a^3 + a}}$
إذن :
$\displaystyle{\displaylines{\forall a \in \left]0, \frac{\pi}{4}\right[ \ : \ -a < \frac{a - \tan(a)}{a^2} < 0}}$
بما أن : $\displaystyle{\displaylines{\lim_{a \rightarrow 0^+ } a = 0}}$
فإن $\displaystyle{\displaylines{ \lim_{a \rightarrow 0^+ } \frac{a - \tan(a)}{a^2} = 0}}$
ومعلوم أن : $\displaystyle{\displaylines{ \lim_{a \rightarrow 0^+ } \frac{\tan^2(a)}{a^2} = \lim_{a \rightarrow 0^+ } \left(\frac{\tan(a)}{a}\right)^2 = 1}}$
وبالتالي :
$\displaystyle{\displaylines{\lim_{a \rightarrow 0^+ } \frac{a - \tan(a)}{\tan^2(a)} = 0}}$
إذن
$\displaystyle{\displaylines{\lim_{x \rightarrow 0^+ } \frac{\arctan(x) - x}{x^2} = 0}}$
بوضع $\displaystyle{\displaylines{ x = -t}}$ نبين أن :
$\displaystyle{\displaylines{\lim_{x \rightarrow 0^- } \frac{\arctan(x) - x}{x^2} = 0}}$
إذن :
$\displaystyle{\displaylines{\color{DarkRed}\lim_{x \rightarrow 0 } \frac{\arctan(x) - x}{x^2} = 0}}$
