) واحدة من أعقد المسائل المفتوحة في الرياضيات، والتي عجز علماء الرياضيات عن حلها رغم المحاولات العديدة للكثير من العلماء المرموقين, وهي تتوقع أن الأصفار الغير بديهية للدالة زيتا في المنطقة الحرجة تملك كلها جزء حقيقي يساوي
. كما أن هذه الخاصية إن صحت ستكون لها نتائج كثيرة على العديد من فروع الرياضيات, كما أن فهمنا لتوزيع هذه الأصفار سيمكننا من فهم توزيع الأعداد الأولية كما سنرى ذلك لاحقا ..
دالة زيتا لمتغير حقيقي
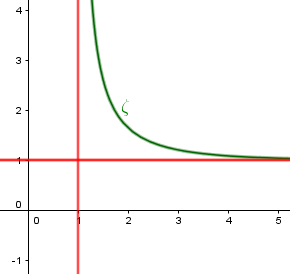
رسم الدالة zeta لمتغير حقيقي.
نُعرف دالة زيتا لـ
أويلر من أجل متغير حقيقي
$\displaystyle{\displaylines{x}}$ كالتالي :
$\displaystyle{\displaylines{\zeta(x) = \sum_{n=1}^{+ \infty} \frac{1}{n^{x}}}}$.
وتكون المتسلسلة متقاربة (
série convergente) إذا وفقط إذا كان
$\displaystyle{\displaylines{x >1}}$.
الحالة
$\displaystyle{\displaylines{x = 1}}$ يكون فيها المجموع متباعد (
série divergente) :
$\displaystyle{\displaylines{1 + \frac{1}{2}+\frac{1}{3}+... = \infty}}$يمكن إثبات أن دالة
$\displaystyle{\displaylines{\zeta}}$ متصلة وقابلة للإشتقاق على المجال
$\displaystyle{\displaylines{]1,+\infty[}}$ على اعتبار أن الحد العام متصل وقابل للإشتقاق و
$\displaystyle{\displaylines{x \rightarrow \dfrac{1}{n^x}}}$ يتقارب بانتظام (
converge uniformément) على
$\displaystyle{\displaylines{[a, +\infty[}}$ بحيث
$\displaystyle{\displaylines{a > 1}}$.
ولدينا
$\displaystyle{\displaylines{\forall x \in ]1, +\infty[ \quad \zeta^{'}(x) = - \sum_{n=2}^{+ \infty} \frac{\ln(n)}{n^{x}}}}$, وبالتالي فالدالة
$\displaystyle{\displaylines{\zeta}}$ تناقصية قطعا على المجال
$\displaystyle{\displaylines{]1, + \infty[}}$.
لدينا أيضا
$\displaystyle{\displaylines{\lim_{x \rightarrow +\infty} \zeta(x) = 1}}$.
ويمكننا بسهولة إثبات المتساوية التالية
$\displaystyle{\displaylines{\forall x >1 \quad \dfrac{1}{x-1} \leq \zeta(x) \leq 1 + \dfrac{1}{x-1}}}$وهو ما يعني أن
$\displaystyle{\displaylines{\lim_{x \rightarrow 1^{+}} (x-1) \zeta(x) = 1}}$.
مشكل Bâle

ليونهارد أويلر (1783-1707)
مشكل
Bâle, هو تحديد القيمة الكاملة للمجموع المتقارب
$\displaystyle{\displaylines{1 +\frac{1}{2^2}+\frac{1}{3^2} + \cdots = \zeta(2)}}$في سنة
1735 وفي محاولة منه لحل مشكل
Bâle وإيجاد قيمة المجموع الغير منتهي
$\displaystyle{\displaylines{1+\frac{1}{2^2}+\frac{1}{3^2} + \cdots = \zeta(2)}}$، اعتبر
Euler "الحدودية"
$\displaystyle{\displaylines{\frac{\sin(x)}{x}}}$ والتي تنعدم في النقط التالية:
$\displaystyle{\displaylines{x_k = k \pi \, , \quad k \in \mathbb{Z}^{*}}}$ .
فكرة
Euler في أنه وجد جميع جذور الحدودية "اللانهائية"
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = 1-\frac{x^2}{3!}+\frac{x^4}{5!}- \cdots}}$.
وهو ما سمح له بكتابة "الحدودية" على شكل جداء لامنتهي:
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = \prod_{k=1}^{+ \infty} \left(1 - \frac{x}{x_k}\right)}}$نقوم بتعويض قيم
$\displaystyle{\displaylines{x_k}}$ :
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = \prod_{k=1}^{+ \infty} \left(1 - \frac{x}{\pi k}\right) \prod_{k=1}^{+ \infty} \left(1 + \frac{x}{\pi k}\right)}}$إذن
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = \prod_{k=1}^{+ \infty} \left(1 - \frac{x^2}{\pi^2 k^2}\right)}}$ وبالتالي
$\displaystyle{\displaylines{\frac{\sin(\pi x)}{\pi x} = \prod_{k=1}^{+ \infty} \left(1 - \frac{x^2}{k^2}\right)}}$وهكذا استطاع
Euler الحصول على الجداء اللانهائي :
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = \left(1-\frac{x^2}{\pi^2}\right) \left(1-\frac{x^2}{\pi^2 2^2}\right) \left(1-\frac{x^2}{\pi^2 3^2}\right) \cdots}}$
بعد القيام بالضرب قام
Euler بتجميع الحدود التي معاملها
$\displaystyle{\displaylines{x^2}}$ :
$\displaystyle{\displaylines{- \left( \frac{1}{\pi^2} + \frac{1}{\pi^2 2^2} + \frac{1}{\pi^2 3^2} + \cdots \right) = - \frac{1}{\pi^2} \sum_{k=1}^{+\infty}\frac{1}{k^2}}}$
وبمقارنة المجموع اللانهائي :
$\displaystyle{\displaylines{\frac{\sin(x)}{x} = 1-\frac{x^2}{3!}+\frac{x^4}{5!}- \cdots}}$
فقد استنتج
Euler النتيجة
$\displaystyle{\displaylines{- \frac{1}{\pi^2} \sum_{k=1}^{+\infty}\frac{1}{k^2} = -\frac{1}{3!}}}$والتي تعني أن
$\displaystyle{\displaylines{\sum_{k=1}^{+\infty}\frac{1}{k^2} = \frac{\pi^2}{6}}}$.
نعلم اليوم أن خطوات
Euler لحساب قيمة
$\displaystyle{\displaylines{\zeta(2)}}$ صحيحة, لكن آنذاك تعرضت طريقة
Euler للتشكيك, لكن
Euler لم يبد اهتمام لها إلا ملاحظة
Bernoulli حول إمكانية وجود أصفار عقدية للـ
$\displaystyle{\displaylines{\sin}}$, وهو ما دفع
Euler لاحقا لاكتشاف العلاقة
$\displaystyle{\displaylines{\exp(ix) = \cos(x) + i \sin(x)}}$ سنة 1748, وهو ما يعني أن دالة
$\displaystyle{\displaylines{\sin}}$ لا تقبل إلا الأصفار الحقيقية
$\displaystyle{\displaylines{x_k}}$.
قيم دالة زيتا للأعداد الصحيحة الطبيعية
بعد حله لمشكل
Bâle وتمكنه من إثبات العلاقة
$\displaystyle{\displaylines{\zeta(2) = \frac{\pi^2}{6}}}$، استطاع
Euler حساب جميع قيم دالة زيتا للأعداد الصحيحة الطبيعية الزوجية في واحدة من أهم أعماله :
$\displaystyle{\displaylines{\zeta(2n) = (-1)^{n+1} \frac{(2\pi)^{2n} B_{2n}}{2 (2n)!}}}$
بحيث
$\displaystyle{\displaylines{B_{2n}}}$ تمثل أعداد برنولي (
nombres de Bernoulli)
$\displaystyle{\displaylines{B_0 = 1, \quad B_1 = \pm \frac{1}{2}, \quad B_2 = \frac{1}{6} , \quad B_4 = - \frac{1}{30} , \cdots}}$أما الأعداد الفردية فلحد الآن لا نعلم أي صيغة لها، كل ما نعرفه الآن هو أن
$\displaystyle{\displaylines{\zeta(3)=1.20205..}}$ عدد لاجذري. وقد تم إثبات ذلك بواسطة
Apéry سنة 1978.
بُرهان
Apéry لم يجد التعميم ليشمل كل الأعداد
$\displaystyle{\displaylines{\zeta(2k+1)}}$, لكن أعمال حثيثة حول هذا البرهان أثبتت أنه توجد مالانهاية من الأعداد
$\displaystyle{\displaylines{\zeta(2k+1)}}$ لاجذرية ضمن قيم دالة زيتا للأعداد الفردية.
البرهان يرجع إلى
Tanguy Rivoal, ومن أجل
$\displaystyle{\displaylines{a}}$ عدد فردي أكبر من
$\displaystyle{\displaylines{3}}$ لدينا:
إذا كان
$\displaystyle{\displaylines{\delta(a)}}$ بُعد الفضاء المتجهي الموجه على
$\displaystyle{\displaylines{\mathbb{Q}}}$ (
$\displaystyle{\displaylines{\mathbb{Q}}}$ l'espace vectoriel engendré sur ) بـ :
$\displaystyle{\displaylines{1, \zeta(3), \zeta(5), \cdots, \zeta(a)}}$فإن
$\displaystyle{\displaylines{\delta(a) \geq \frac{\log(a)}{3}}}$وبما أن
$\displaystyle{\displaylines{\lim_{a \rightarrow +\infty} \delta(a) \geq \lim_{a \rightarrow +\infty} \frac{\log(a)}{3} = + \infty}}$, فإنه توجد مالانهاية من قيم زيتا للأعداد الفردية لاجذرية. ويحدس العلماء اليوم أن جميع قيم زيتا الفردية لاجذرية ومتسامية أيضا.
| $\displaystyle{\displaylines{n}}$ | | $\displaystyle{\displaylines{\zeta(n)}}$ قيمة | | التقريبية | الكاملة |
| لاجذري
irrationnel | متسامي
transcendant |
| $\displaystyle{\displaylines{2}}$ | | $\displaystyle{\displaylines{1,6449...}}$ | $\displaystyle{\displaylines{\frac{\pi^2}{6}}}$ |
| نعم | نعم |
| $\displaystyle{\displaylines{3}}$ | | $\displaystyle{\displaylines{1,2020...}}$ | ? |
| نعم | ? |
| $\displaystyle{\displaylines{4}}$ | | $\displaystyle{\displaylines{1,0823...}}$ | $\displaystyle{\displaylines{\frac{\pi^4}{90}}}$ |
| نعم | نعم |
| $\displaystyle{\displaylines{5}}$ | | $\displaystyle{\displaylines{1,0369...}}$ | ? |
| ? | ? |
| $\displaystyle{\displaylines{6}}$ | | $\displaystyle{\displaylines{1,0173...}}$ | $\displaystyle{\displaylines{\frac{\pi^6}{945}}}$ |
| نعم | نعم |
| $\displaystyle{\displaylines{7}}$ | | $\displaystyle{\displaylines{1,0083...}}$ | ? |
| ? | ? |
| ... | | | |
| $\displaystyle{\displaylines{2 k}}$ | $\displaystyle{\displaylines{\zeta(2k) = (-1)^{k+1} \frac{(2\pi)^{2k} B_{2k}}{2 (2k)!}}}$ | نعم | نعم |
| $\displaystyle{\displaylines{2k+1}}$ | ? | ? | ? |
جداء أويلر
في سنة 1737 استطاع
Euler باستغلال المبرهنة الأساسية للحسابيات التي تقول على أن كل عدد صحيح يمكن كتابته بشكل وحيد على شكل جداء عوامل أولية من إثبات أولى العلاقات للدالة زيتا مع الأعداد الأولية :
$\displaystyle{\displaylines{\zeta(x) = \prod_{\text{p premier}} \frac{1}{1 - p^{-x}} , \quad x > 1}}$
بحيث الجداء على مجموعة الأعداد الأولية, لدينا :
$\displaystyle{\displaylines{\zeta(x) = \frac{1}{1 - 2^{-x}} \frac{1}{1 - 3^{-x}} \frac{1}{1 - 5^{-x}} ...}}$علاقة
Euler الجديدة تمثل إثبات آخر للا نهائية الأعداد الأولية, حيث تباعد دالة
$\displaystyle{\displaylines{\zeta}}$ في
$\displaystyle{\displaylines{x = 1}}$ يبين ذلك :
$\displaystyle{\displaylines{\sum_{k=1}^{+\infty} \frac{1}{k} = \prod_{\text{p premier}} \frac{p}{p-1} = \infty}}$
كما أن هذه العلاقة سمحت لـ
أويلر من إثبات تباعد متسلسلة مقلوب الأعداد الأولية :
$\displaystyle{\displaylines{\sum_{\text{p premier}} \frac{1}{p} = \frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\cdots= \infty}}$
دالة زيتا المتناوبة
نُعرف دالة زيتا المتناوبة (
zeta alternée) كالتالي :
$\displaystyle{\displaylines{\eta(x) = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}}{n^x}}}$دالة زيتا المتناوبة تُسمى أيضا دالة إيتا
fonction êta de Dirichlet.
بما أن الحد العام للمتسلسلة متناوب (
alterné), فإنه يكفي أن يؤول إلى الصفر ليتقارب المجموع.
وبالتالي فإن مجال تعريف
$\displaystyle{\displaylines{\eta}}$ هو
$\displaystyle{\displaylines{\mathbb{R}^{*}_{+}}}$.
هناك علاقة تربط بين
$\displaystyle{\displaylines{\zeta}}$ و
$\displaystyle{\displaylines{\eta}}$ يمكن إثباتها بسهولة :
$\displaystyle{\displaylines{\zeta(x) = \frac{\eta(x)}{1-2^{1-x}}}}$لاحظ أن مجال تعريف الدالة
$\displaystyle{\displaylines{x \rightarrow \frac{\eta(x)}{1-2^{1-x}}}}$ هو
$\displaystyle{\displaylines{\mathbb{R}^{*}_{+} - \{1\}}}$وهو ما يسمح بتمديد مجال تعريف الدالة
$\displaystyle{\displaylines{\zeta}}$ ليشمل
$\displaystyle{\displaylines{\mathbb{R}^{*}_{+} - \{1\}}}$. لدينا :
$\displaystyle{\displaylines{\zeta(x) = \left\{ \begin{array}{cl}\displaystyle\sum_{n=1}^{+\infty} \frac{1}{n^x} & : \ x >1 \\ \\\dfrac{\eta(x)}{1-2^{1-x}}& : \ 0<x < 1\end{array} \right.}}$
هذا التمديد ضروري جدا في اكتشاف أسرار دالة زيتا والذي يمكننا تمديده أكثر ليشمل
$\displaystyle{\displaylines{\mathbb{R}-\{1\}}}$ كما سنرى لاحقا في دالة زيتا لـ
ريمان.
كما بينا سابقا لدينا :
$\displaystyle{\displaylines{\displaystyle\lim_{x \rightarrow 1^{+}} (x-1) \zeta(x) = 1}}$, الآن لنحسب النهاية لكن على يسار النقطة
$\displaystyle{\displaylines{x=1}}$.
$\displaystyle{\displaylines{\begin{array}{rcl}\displaystyle\lim_{x \rightarrow 1^{-}} (x-1) \zeta(x) & = & \displaystyle\lim_{x \rightarrow 1^{-}} \dfrac{(x-1)}{1-2^{1-x}} \eta(x) \\& = & \dfrac{\ln(2)}{\ln(2)} \\& = & 1 \end{array}}}$
يكفي ملاحظة أنه لدينا :
$\displaystyle{\displaylines{\eta(1) = \sum_{n=1}^{+\infty}\frac{(-1)^{n+1}}{n} = \ln(2)}}$ وأيضا الخاصية
$\displaystyle{\displaylines{\displaystyle\lim_{h \rightarrow 0} \dfrac{2^h - 1}{h} = \ln(2)}}$خلاصة : $\displaystyle{\displaylines{\lim_{x \rightarrow 1} (x-1) \zeta(x) = 1}}$دالة زيتا لمتغير عقدي

برنارد ريمان (1866-1826)
يُعتبر
برنارد ريمان أول من درس دالة
$\displaystyle{\displaylines{\zeta}}$ من أجل متغير عقدي
$\displaystyle{\displaylines{s \in \mathbb{C}}}$.
وقد استفاد
Riemann من تطور نظرية التحليل العقدي على يد علماء بارزين مثل
Cauchy (1789-1857) و
Carle Weierstrass (1815-1897) وهو أيضا, إذ يُعتبر
Riemann من مؤسسي هذا الفرع في الرياضيات.
ونظرية التحليل العقدي تدرس الدوال ذات المتغير العقدي (
variable complexe), كما أنها تدرس سلوك المتسلسلات ذات المتغير العقدي من تقارب (
convergence) أو تباعد (
Divergence) بالإضافة لقابلية الإشتقاق(الدوال الهولومرفية) والتكامل وتحديد الأصفار (النقط التي تنعدم فيها الدالة) والأقطاب (النقط التي تؤول فيها إلى مالانهاية والتي تكون قسمة على صفر), بالإضافة لتمديد مجال تعريف الدوال العقدية في ما يسمى بالتمديد التحليلي (
prolongement analytique) .
وسائل
Riemann الجديدة والتي لم تكن متوفرة لدى
Euler مكنته من دراسة دالة
$\displaystyle{\displaylines{\zeta}}$ على مجالات أخرى وإيجاد علاقات وأسرار غامضة تثبت علاقة دالة زيتا الوثيقة مع الأعداد الأولية.
دالة زيتا من أجل متغير عقدي :$\displaystyle{\displaylines{\zeta(s) = \sum_{n=1}^{+\infty} \frac{1}{n^s} \, , \quad \Re(s) > 1}}$
دالة زيتا لـ
ريمان تتقارب مطلقا (
converge Absolument) من أجل
$\displaystyle{\displaylines{\Re(s) > 1}}$.
وذلك واضح من خلال
$\displaystyle{\displaylines{\left| \frac{1}{n^s} \right| = \frac{1}{n^{\Re(s)}}}}$, وكما رأينا سابقا فإن المتسلسلة
$\displaystyle{\displaylines{\sum \frac{1}{n^{\Re(s)}}}}$ تتقارب من أجل
$\displaystyle{\displaylines{\Re(s) > 1}}$.
دالة زيتا هولومرفية (
holomorphe) على المجموعة
$\displaystyle{\displaylines{\{s \in \mathbb{C} \, | \, \Re(s) > 1\}}}$, وبالتالي فهي تحليلة على هذه المجموعة (
analytique) حسب مبرهنة
Cauchy.
جداء Euler :
$\displaystyle{\displaylines{\zeta(s) = \prod_{\text{p premier}} \frac{1}{1 - p^{-s}} , \quad \Re(s) > 1}}$
دالة زيتا المتناوبة :
$\displaystyle{\displaylines{\eta(s) = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}}{n^s} \, , \quad \Re(s) > 0}}$
من خلال العلاقة
$\displaystyle{\displaylines{\zeta(s) = \frac{\eta(s)}{1-2^{1-s}}}}$ يمكننا تمديد مجال تعريف الدالة زيتا ليشمل نصف المستوى العقدي
$\displaystyle{\displaylines{\Re(s) > 0}}$ باستثناء النقطة
$\displaystyle{\displaylines{s = 1}}$ التي تمثل قطبا بسيطا (
pôle simple).
التمديد التحليلي لدالة زيتا
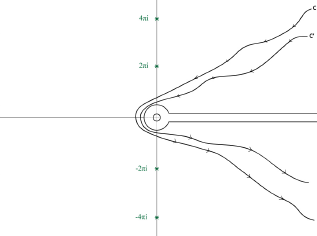
منحنى Riemann
مكنت كتابة الدالة
$\displaystyle{\displaylines{\zeta}}$ على شكل تكامل منحني
Riemann من تمديد دالة
$\displaystyle{\displaylines{\zeta}}$ تحليليا لتشمل كامل المستوى العقدي باستثناء
$\displaystyle{\displaylines{s=1}}$ التي تمثل قطبا بسيطا.
$\displaystyle{\displaylines{\zeta(s) = \frac{e^{i \pi s} \Gamma(1-s)}{2 i \pi} \oint_{C} \dfrac{u^{s-1}}{e^{u} - 1} du}}$
بحيث
$\displaystyle{\displaylines{C}}$ يمثل منحنى على طول المستقيم الحقيقي يشمل أصل المعلم ويتحرك من
$\displaystyle{\displaylines{+\infty}}$ نحو
$\displaystyle{\displaylines{+\infty}}$ في الإتجاه المثلثي.
رسم الدالة gamma على IR
تمثل دالة غاما لـ
أويلر وهي دالة معرفة من أجل
$\displaystyle{\displaylines{\Re(s) > 0}}$, وتقبل تمديدا لدالة ميرومورفية بفضل العلاقة
$\displaystyle{\displaylines{\Gamma(z+1) = z \Gamma(z)}}$, مع وجود أقطاب في النقط
$\displaystyle{\displaylines{0,-1,-2, \cdots}}$.
لاحظ أن الدالة
$\displaystyle{\displaylines{\Gamma}}$ تعتبر تمديد
$\displaystyle{\displaylines{n!}}$ في
$\displaystyle{\displaylines{\mathbb{C}-\{0,-1,-2,\cdots\}}}$.
لدينا
$\displaystyle{\displaylines{\Gamma(1) = 1}}$ و
$\displaystyle{\displaylines{\forall n \in \mathbb{N}^{*} \quad \Gamma(n) = (n-1)!}}$العلاقة أعلاه أتبثت أن الدالة
$\displaystyle{\displaylines{\zeta}}$ منتظمة (
uniforme) ومنتهية من أجل أي قيمة
$\displaystyle{\displaylines{s \in \mathbb{C}-\{1\}}}$.
وهو ما مكن من إثبات التمديد التحليلي للدالة
$\displaystyle{\displaylines{\zeta}}$ بشكل وحيد على كامل المستوى العقدي باستثناء
$\displaystyle{\displaylines{s=1}}$.
طموح
Riemann لم يقف عند هذا الحد, فاعتمادا على علاقة افترضها
Euler, تمكن
Riemann من إثباتها رياضيا :
$\displaystyle{\displaylines{\zeta(s) = 2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \, , \quad 0 < \Re(s) < 1}}$
العلاقة أعلاه لم تعط برهانا آخر لتمديد الدالة
$\displaystyle{\displaylines{\zeta}}$ فقط لتصبح دالة ميرومورفية (دالة هولومرفية على كامل المستوى العقدي باستثناء أقطاب الدالة) بل ساعدت في معرفة بعض أصفار الدالة وخصائصها كما سنرى لاحقا.
بالنسبة للنقطة
$\displaystyle{\displaylines{s = 0}}$ وباعتبار النهاية
$\displaystyle{\displaylines{\lim_{s \rightarrow 0^{+}} \zeta(s)}}$
$\displaystyle{\displaylines{ \begin{array}{rcl}\displaystyle\lim_{s \rightarrow 0^{+}} \zeta(s) & = & \displaystyle\lim_{s \rightarrow 0^{+}} 2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \\& = & \displaystyle\lim_{s \rightarrow 0^{+}} \dfrac{1}{s \pi} \sin\left(\dfrac{\pi s}{2}\right) s \, \zeta(1-s) \\& = & -\dfrac{1}{2} \end{array}}}$
وبالتالي
$\displaystyle{\displaylines{\zeta(0) = -\dfrac{1}{2}}}$خلاصة :$\displaystyle{\displaylines{\zeta(s) = 2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \, , \quad s \in \mathbb{C}-\{1\}}}$
دالة زيتا لريمان :$\displaystyle{\displaylines{\zeta(s) = \left\{ \begin{array}{cl}\displaystyle\sum_{n=1}^{+\infty} \dfrac{1}{n^s} & : \ \Re(s)>1 \\ \\\dfrac{\eta(s)}{1-2^{1-s}} & : \ 0 \leq \Re(s) \leq 1 \\ \\2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) & : \ \Re(s) < 0\end{array} \right.}}$
ملاحظة هامة: دراستنا الآن حول دالة زيتا ستتمحور حول كامل المستوى العقدي
$\displaystyle{\displaylines{\mathbb{C}-\{1\}}}$, مع ملاحظة أن مجموعة النقط
$\displaystyle{\displaylines{x(t) = 1 + i t}}$ بحيث
$\displaystyle{\displaylines{t \in \mathbb{R}^{*}}}$ معرفة على مجال تعريف الدالة
$\displaystyle{\displaylines{\zeta}}$.
فقط النقطة
$\displaystyle{\displaylines{x(t=0)=1}}$ غير معرفة وتمثل قطبا بسيطا.
قيم دالة زيتا للأعداد الصحيحة السالبة
ليكن
$\displaystyle{\displaylines{n \in \mathbb{N}}}$ :

إذا كان
$\displaystyle{\displaylines{n = 0}}$ فإن
$\displaystyle{\displaylines{\zeta(0) = - \dfrac{1}{2}}}$.

إذا كان
$\displaystyle{\displaylines{n}}$ زوجي
$\displaystyle{\displaylines{n = 2k}}$ لدينا :
$\displaystyle{\displaylines{\begin{array}{rcl}\zeta(-n) & = & \zeta(-2k) \\ \\& = & 2^{-(2k)} \pi^{-2k-1} \sin(- k \pi) \Gamma(1+2k) \zeta(1+2k) \\ \\& = & 0 \end{array}}}$

إذا كان
$\displaystyle{\displaylines{n}}$ فردي
$\displaystyle{\displaylines{n = 2k+1}}$ لدينا :
يجب تذكر القيمة التي ذكرناها في فقرة "
دالة زيتا لـأويلر" :
$\displaystyle{\displaylines{\forall k \in \mathbb{N}^{*} \quad \zeta(2k) = (-1)^{k+1} \frac{(2\pi)^{2k} B_{2k}}{2 (2k)!}}}$$\displaystyle{\displaylines{\begin{array}{rcl}\zeta(-n) & = & \zeta(-(2k+1)) \\ \\& = & 2^{-2k-1} \pi^{-2k-2} \sin\left(\dfrac{- (2k+1) \pi}{2}\right) \Gamma(2k+2) \zeta(2(k+1)) \\ \\& = & 2^{-2k-1} \pi^{-2k-2} (-1)^{k} (2k+1)! (-1)^{k+1} \dfrac{(2\pi)^{2k+2} B_{2k+2}}{2 (2k+2)!}\\ \\& = & - \dfrac{B_{2k+2}}{2k+2} \\ \\& = & - \dfrac{B_{n+1}}{n+1}\end{array}}}$
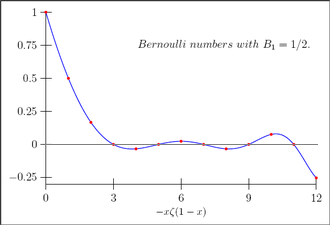
رسم يوضح قيم أعداد برنولي بواسطة دالة زيتا لريمان
وبصفة عامة وبما أن
أعداد برنولي تنعدم عند الأعداد الفردية لدينا :
$\displaystyle{\displaylines{\forall n \in \mathbb{N}^{*} \quad \zeta(-n) = (-1)^n \dfrac{B_{n+1}}{n+1}}}$
وبما أن
$\displaystyle{\displaylines{\zeta(0) = -\dfrac{1}{2} = B_1}}$ فإن العلاقة تبقى صحيحة من أجل
$\displaystyle{\displaylines{n=0}}$.
خلاصة : قيم الدالة
$\displaystyle{\displaylines{\zeta}}$ من أجل الأعداد الصحيحة السالبة :
$\displaystyle{\displaylines{\forall n \in \mathbb{N}\quad \zeta(-n) = (-1)^n \dfrac{B_{n+1}}{n+1}}}$
وهذه طريقة لاستنتاج
أعداد برنولي انطلاقا من دالة زيتا :
$\displaystyle{\displaylines{\forall n \in \mathbb{N} \quad B_n = - n \zeta(1-n)}}$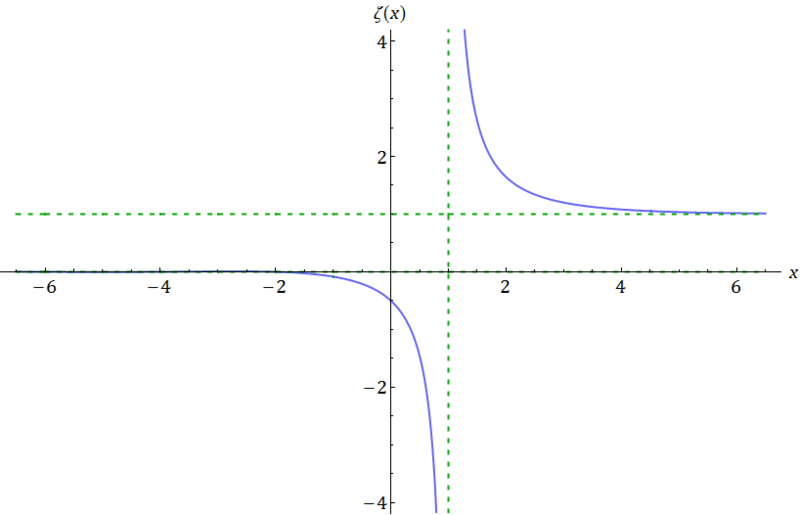
رسم الدالة زيتا لمتغير حقيقي (بعد التمديد) بين النقطتين -7 و 7.
أصفار الدالة زيتا
واحدة من أدوار التحليل العقدي هي دراسة النقط التي تنعدم فيها الدوال.
لذلك سندرس في هذه الفقرة النقط
$\displaystyle{\displaylines{s\in\mathbb{C}-\{1\}}}$ بحيث
$\displaystyle{\displaylines{\zeta(s) = 0}}$.
ليكن
$\displaystyle{\displaylines{s \in \mathbb{C}-\{1\}}}$ :
 إذا كان $\displaystyle{\displaylines{\Re(s) > 1}}$
إذا كان $\displaystyle{\displaylines{\Re(s) > 1}}$ :
لدينا العلاقة $\displaystyle{\displaylines{\zeta(s)=\prod_{\text{p premier}} \frac{1}{1 - p^{-s}}}}$ تستلزم أن الدالة زيتا لا تنعدم.
خلاصة: الدالة $\displaystyle{\displaylines{\zeta}}$ لا تنعدم إذا كان $\displaystyle{\displaylines{\Re(s) > 1}}$.
 إذا كان $\displaystyle{\displaylines{\Re(s) < 0}}$
إذا كان $\displaystyle{\displaylines{\Re(s) < 0}}$ :
لدينا العلاقة : $\displaystyle{\displaylines{\zeta(s) = 2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s)}}$
وبما أن $\displaystyle{\displaylines{\Re(s) < 0}}$ فإن $\displaystyle{\displaylines{\Re(1-s)>1}}$, ومنه $\displaystyle{\displaylines{s \rightarrow \zeta(1-s)}}$ لا تقبل أي أصفار كما رأينا سابقا.
لدينا أيضا $\displaystyle{\displaylines{s \rightarrow 2^s \pi^{s-1} \Gamma(1-s)}}$ لا تقبل أي أصفار.
لدينا الدالة $\displaystyle{\displaylines{s \rightarrow \sin\left(\dfrac{\pi s}{2}\right)}}$ تنعدم في النقط $\displaystyle{\displaylines{x_k = -2k \, , \quad k \in \mathbb{N}^{*}}}$.
نقول أن النقط $\displaystyle{\displaylines{-2,-4,-6,-8, \cdots}}$ أنها أصفار بديهية, لأنها تظهر بوضوح في صيغة العلاقة الدالية لدالة $\displaystyle{\displaylines{\zeta}}$.
خلاصة: الدالة $\displaystyle{\displaylines{\zeta}}$ تنعدم في النقط الزوجية السالبة قطعا ($\displaystyle{\displaylines{-2,-4,-6,-8, \cdots}}$) إذا كان $\displaystyle{\displaylines{\Re(s) < 0}}$.
 إذا كان $\displaystyle{\displaylines{0 \leq \Re(s) \leq 1}}$
إذا كان $\displaystyle{\displaylines{0 \leq \Re(s) \leq 1}}$ :
في سنة 1896 تمكن كل من
Hadamard و
de la Vallée Poussin من إثبات وبشكل مستقل أن الدالة
$\displaystyle{\displaylines{\zeta}}$ لا تنعدم من أجل
$\displaystyle{\displaylines{\Re(s)=1}}$ وبشكل مماثل ومن خلال العلاقة الدالية فإنها لا تنعدم أيضا من أجل
$\displaystyle{\displaylines{\Re(s) = 0}}$, هذه النتيجة سوف نرى لاحقا كيف أن لها تأثير على سلوك دالة حساب عدد الأعداد الأولية الأصغر من
$\displaystyle{\displaylines{x}}$.
في سنة 1914 تمكن
Hardy واعتمادا على نتيجة عامة في التحليل العقدي من إثبات أن دالة
$\displaystyle{\displaylines{\zeta}}$ تنعدم في مالا نهاية من النقط من أجل
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$ :
من أجل
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$ نعتبر الدالة التالية :
$\displaystyle{\displaylines{\xi(s) = \dfrac{1}{2} s (s-1) \pi^{-\frac{s}{2}} \Gamma(\dfrac{s}{2}) \zeta(s)}}$
اعتمادا على العلاقة الدالية لـ
$\displaystyle{\displaylines{\zeta}}$ لدينا :
$\displaystyle{\displaylines{\xi(s) = \xi(1-s)}}$
وباعتبار الدالة :
$\displaystyle{\displaylines{\Xi(s) = \xi (\dfrac{1}{2} + i s)}}$
فإنها تحقق العلاقة
$\displaystyle{\displaylines{\Xi(-s) = \Xi(s)}}$ وبالتالي فإنها زوجية.
يمكننا إثبات أن
$\displaystyle{\displaylines{\xi}}$ و
$\displaystyle{\displaylines{\Xi}}$ دالتين صحيحتين (
fonctions entières) من الرتبة
$\displaystyle{\displaylines{1}}$.
وبما أن
$\displaystyle{\displaylines{\Xi}}$ دالة زوجية فإن
$\displaystyle{\displaylines{s \rightarrow \Xi(\sqrt{s})}}$ دالة صحيحة من الرتبة
$\displaystyle{\displaylines{\frac{1}{2}}}$ :
ومنه وحسب المبرهنة العامة للدوال الصحيحة, فإن الدالة $\displaystyle{\displaylines{s \rightarrow \Xi(\sqrt{s})}}$ تقبل مالانهاية من الأصفار.رجوعا إلى الدالة
$\displaystyle{\displaylines{\zeta}}$ فإنها تقبل مالانهاية من الأصفار من أجل
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$.
هذه الأصفار تسمى
أصفارا غير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$ لأننا لا نعلم بالتحديد كم تساوي أو أين توجد, كل ما نعلمه أنها تحقق
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$ وأشياء قليلة سنذكرها بعد قليل.
خلاصة: الدالة
$\displaystyle{\displaylines{\zeta}}$ تقبل مالانهاية من الأصفار من أجل
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$.
كما قلنا سابقا فإن الدالة
$\displaystyle{\displaylines{\zeta}}$ ميرومورفية (هولومرفية على
$\displaystyle{\displaylines{\mathbb{C}}}$ باستثناء الأقطاب), وأنها تقبل مالانهاية من الأصفار, وبالتالي فإنه وحسب مبرهنة
Hadamard يمكن كتابتها على شكل جداء تظهر فيه جميع الأصفار والأقطاب :
$\displaystyle{\displaylines{\zeta(s) = \dfrac{(2 \pi)^{s} e^{- (1 + \frac{\gamma}{2}) s}}{2 (s-1) \Gamma(1+\frac{s}{2})} \prod_{\rho} \left( 1 - \frac{s}{\rho} \right) e^{s/\rho}}}$
بحيث الجداء على مجموعة الأصفار الغير بديهية
$\displaystyle{\displaylines{\rho}}$.
$\displaystyle{\displaylines{\gamma}}$ تمثل ثابتة
Euler-Mascheroni :
$\displaystyle{\displaylines{\gamma = \lim_{n \rightarrow + \infty} \sum_{k=1}^{n}\dfrac{1}{k} - \ln(n) = 0.5772 \cdots}}$ويمكن ملاحظة أن الأصفار البديهية ممثلة من خلال الدالة
$\displaystyle{\displaylines{\Gamma}}$, إذ يكفي ملاحظة أن
$\displaystyle{\displaylines{\Gamma(1 + \frac{-2k}{2}) = \pm \infty}}$ من أجل
$\displaystyle{\displaylines{k \in \mathbb{N}^{*}}}$.
المنطقة
$\displaystyle{\displaylines{0 < \Re(s) < 1}}$ تسمى المنطقة الحرجة (
bande critique).
كما أن المستقيم
$\displaystyle{\displaylines{\Re(s) = \frac{1}{2}}}$ يسمى المستقيم الحرج (
droite critique).
فرضية ريمان
فرضية ريمان هي واحدة من أهم المسائل المفتوحة في الرياضيات وأعقدها على الإطلاق.
هذه الفرضية لصاحبها
Riemann تقول أن جميع الأصفار الغير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$ تملك جزء حقيقي يساوي
$\displaystyle{\displaylines{\frac{1}{2}}}$.

دافيد هيلبرت (1943-1862)
أثناء المؤتمر الدولي الثاني للرياضيات في باريس سنة 1900 والذي اجتمع فيه خيرة الرياضيين آنذاك, عرض
David Hilbert على المجتمع الرياضي 23 مسألة مفتوحة فيما سمي بـ
معضلات هيلبرت, واحتلت فيه فرضية ريمان بالإضافة لـ
حدسية غولدباخ وفرضية الأعداد الأولية التوأم الرقم 8 من هذه المسائل.
ومنذ ذلك الحين انكب بعض العلماء محاولين إثبات هذه الفرضية المستعصية لكن دون جدوى, وقد غيروا بوصلتهم قليلا في اتجاه التحقق الرقمي لتجربة الفرضية, حيث تمكن
Gram سنة 1903 من حساب
$\displaystyle{\displaylines{15}}$ صفر غير بديهي وأثبت أن جميعها لها جزء حقيقي يساوي
$\displaystyle{\displaylines{\frac{1}{2}}}$.
التحقق الرقمي لم يقف هنا فقد تمكن
Backlund سنة 1914 من حساب
$\displaystyle{\displaylines{79}}$ صفر غير بديهي وتحقق جميعها
فرضية ريمان.
وقد عرف التحقق الرقمي لـفرضية ريمان منعطفا هاما على يد
Alan Turing الذي أدخل هذا التحقق للحاسوب عوض التحقق اليدوي الذي كان يتطلب عملا شاقا.
وصل التحقق الرقمي لأصفار دالة زيتا سنة 2004 إلى
$\displaystyle{\displaylines{10^{13}}}$ صفر وكلها تقع في المستقيم الحرج.
بعد مرور قرن على عقد مؤتمر
هيلبرت عرفت العديد من مسائله طريقها نحو الحل, فيما بقيت بعضها مستعصية! لهذا قام معهد كلاي سنة 2000 بطرح سبعة مسائل مفتوحة في ما سمي بمسائل القرن, وواحدة من هذه المسائل
فرضية ريمان طبعا..
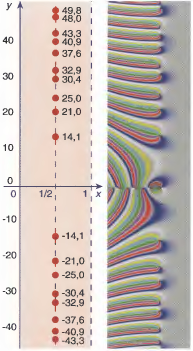
أولى الأصفار الغير بديهية للدالة زيتا في النطاق الحرج
إشكالية الأصفار الغير بديهية تتجلى في أننا لا نعلم أي صيغة يمكن أن نعرف بها كم تساوي بالضبط, كل ما نملكه الآن هو طرق رقمية لحسابها وهذه أولى الأصفار التي تحقق
$\displaystyle{\displaylines{\zeta(\rho) = 0}}$ :
$\displaystyle{\displaylines{ \begin{array}{rcl}\rho_{1} & = & 0.5 \pm i 14.13472 \cdots \\\rho_{2} & = & 0.5 \pm i 21.02203\cdots \\\rho_{3} & = & 0.5 \pm i 25.01085\cdots \\\rho_{4} & = & 0.5 \pm i 30.42487\cdots \\\rho_{5} & = & 0.5 \pm i 32.93506\cdots\end{array}}}$
فخلافا للأصفار البديهية التي استنتجناها من العلاقة الدالية لـ
$\displaystyle{\displaylines{\zeta}}$ :
$\displaystyle{\displaylines{\zeta(s) = 2^s \pi^{s-1} \sin\left(\dfrac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \, , \quad s \in \mathbb{C}-\{1\}}}$
فإن العلاقة الدالية تمكننا فقط من إثبات أنه وإذا كان
$\displaystyle{\displaylines{\zeta(\rho) = 0}}$ فإنه كذلك
$\displaystyle{\displaylines{\zeta(1-\rho) = 0}}$.
وكذلك العلاقة
$\displaystyle{\displaylines{\overline{\zeta(\rho)} = \zeta(\overline{\rho})}}$ وهو ما يعني أن جميع الأصفار داخل المنطقة الحرجة متماثلة بالنسبة للمستقيم
$\displaystyle{\displaylines{x = \frac{1}{2}}}$.
عدد الأصفار الأصغر من T
ليكن
$\displaystyle{\displaylines{N(T)}}$ عدد الأصفار الغير بديهية بحيث
$\displaystyle{\displaylines{\rho_n = \sigma_n + i \delta_n}}$ و
$\displaystyle{\displaylines{\delta_n \leq T}}$.
اعتمادا على بعض الملاحظات, خمن
Riemann العلاقة التالية :
$\displaystyle{\displaylines{N(T) = \dfrac{T}{2 \pi} \ln(\dfrac{T}{2 \pi e}) + O(\ln(T))}}$
هذه العلاقة تم إثباتها لاحقا بواسطة
Von Mongoldtوقد بينت هذه العلاقة التقريب
$\displaystyle{\displaylines{\delta_n \approx \pm \frac{2 \pi n}{\ln(n)}}}$.
فرضية ريمان تكافئ أن المنطقة
$\displaystyle{\displaylines{\frac{1}{2} < \Re(s) < 1}}$ لا تحتوي على أصفار, وذلك واضح لأن الأصفار كما قلنا أنها متماثلة بالنسبة للمستقيم الحرج
$\displaystyle{\displaylines{x=\frac{1}{2}}}$, فإذا كانت جميع الأصفار توجد فقط في
$\displaystyle{\displaylines{0 < \Re(s) \leq \frac{1}{2}}}$ فإنها توجد إذن في الجزء الحقيقي
$\displaystyle{\displaylines{\frac{1}{2}}}$.
نعرف
$\displaystyle{\displaylines{N_{0}(T)}}$ بــعدد الأصفار الموجودة في المستطيل بين
$\displaystyle{\displaylines{0}}$ و
$\displaystyle{\displaylines{\frac{1}{2}}}$ و بالطول
$\displaystyle{\displaylines{T}}$.
فرضية ريمان تكافئ
$\displaystyle{\displaylines{N_{0}(T) = N(T)}}$نعلم وجود ثابتة
$\displaystyle{\displaylines{c}}$ بحيث :
$\displaystyle{\displaylines{\forall T \geq 2 \qquad c \, N(T) \leq c \, T \ln(T) \leq N_{0}(T)}}$
لا نعلم أي قيمة رقمية للثابتة
$\displaystyle{\displaylines{c}}$.
تمكن
Conrey سنة 1989 من إثبات :
$\displaystyle{\displaylines{\lim_{T \rightarrow +\infty} \inf \frac{N_{0}(T)}{N(T)} \geq 0,4077}}$
هذه العلاقة تثبت أن عدد الأصفار الغير بديهية التي جزءها الحقيقي يساوي
$\displaystyle{\displaylines{\frac{1}{2}}}$ غير منتهية وأنها تساوي %40 على الأقل من مجموع الأصفار الغير بديهية.
منطقة بدون أصفار
في محاولة لحل المشكلة, فكر العلماء في طريقة لتقليص قطر المنطقة الحرجة للاقتراب أكثر من الفرضية.
كما هو معلوم فإن العالم
de la Vallée Poussin تمكن من إثبات أن
$\displaystyle{\displaylines{\zeta}}$ لا تنعدم من أجل
$\displaystyle{\displaylines{\Re(s) = 1}}$, وقد تمكن سنة 1899 من توسيع هذه النتيجة, دالة
$\displaystyle{\displaylines{\zeta}}$ لا تنعدم إذا كان :
$\displaystyle{\displaylines{\Re(s) \geq 1 - \frac{c}{\ln(t)}, \quad t = |\Im(s)| \geq 2 , \quad c = \frac{1}{34.82}}}$

Charles Jean de la Vallée Poussin (1866-1962)
معرفة المنطقة بدون أصفار ضرورية جدا في معرفة نسبة الخطأ في تقدير بعض الدوال الحسابية كما سنرى لاحقا.
لاحظ أنه في صيغة
de la Vallée Poussin كلما كان
$\displaystyle{\displaylines{c}}$ أكبر كلما كانت المنطقة بدون أصفار أحسن.
تمكن
Rosser سنة 1941 من تحسين قيمة
$\displaystyle{\displaylines{c = \frac{1}{19}}}$تمكن
K.Ford أيضا من تحسين النتيجة
$\displaystyle{\displaylines{c = \frac{1}{8.463}}}$أحسن نتيجة محصلة الآن من أجل
$\displaystyle{\displaylines{c = \frac{1}{5.69693}}}$مكنت أعمال كل من
Korobov و
Vinogradov من إيجاد منطقة أخرى بدون أصفار:
$\displaystyle{\displaylines{\Re(s) \geq 1 - \frac{k}{\ln(t)^{2/3} \ln(\ln(t))^{1/3}} , \quad t = |\Im(s)| \geq 10}}$
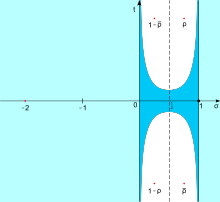
أكبر منطقة بدون أصفار معروفة (اللون الأزرق)
سنة 1994 أثبت
O. V. Popov أن
$\displaystyle{\displaylines{k = \frac{1}{14518}}}$ تحقق المتفاوتة.
سنة 2000 استطاع
Y. Cheng تحسين النتيجة
$\displaystyle{\displaylines{k = \frac{1}{990}}}$أحسن نتيجة تعود إلى
K.Ford من أجل
$\displaystyle{\displaylines{k = \frac{1}{57.54}}}$تعتبر منطقة
de la Vallée Poussin بالنظر إلى قيم
$\displaystyle{\displaylines{k}}$ و
$\displaystyle{\displaylines{c}}$ الحالية أحسن من منطقة
Vinogradov-Korobov حتى
$\displaystyle{\displaylines{t = e^{9402.562}}}$.
العلاقة مع دالة Mertens
باستغلال جداء
Euler يمكننا إثبات المتساوية التالية :
$\displaystyle{\displaylines{\dfrac{1}{\zeta(s)} = \prod_{\text{p premier}} \left({1 - \frac{1}{p^s}}\right) = \sum_{n=1}^{+ \infty} \dfrac{\mu(n)}{n^s}, \quad \Re(s) > 1}}$
بحيث
$\displaystyle{\displaylines{\mu}}$ تمثل دالة
Möbius, وهي دالة حسابية معرفة كالتالي :
- $\displaystyle{\displaylines{\mu(1)=1}}$
- $\displaystyle{\displaylines{\mu(n)=0}}$ إذا كان $\displaystyle{\displaylines{n}}$ يقبل مربع عدد أولي كقاسم.
- $\displaystyle{\displaylines{\mu(n)=1}}$ إذا كان $\displaystyle{\displaylines{n}}$ يقبل عدد زوجي من القواسم الأولية وكلها أس $\displaystyle{\displaylines{1}}$.
- $\displaystyle{\displaylines{\mu(n)=-1}}$ إذا كان $\displaystyle{\displaylines{n}}$ يقبل عدد فردي من القواسم الأولية وكلها أس $\displaystyle{\displaylines{1}}$.
اعتمادا على صيغة
Perron و تبديل
Mellin يمكن إثبات واعتمادا على المجموع الجديد أن :
$\displaystyle{\displaylines{\dfrac{1}{\zeta(s)} = s \int_{1}^{+ \infty} \dfrac{M(x)}{x^{s+1}} dx , \quad \Re(s) > 1}}$
بحيث
$\displaystyle{\displaylines{M}}$ تمثل دالة
Mertens :
$\displaystyle{\displaylines{M(x) = \sum_{n \leq x} \mu(n)}}$العلاقة تبقى صحيحة من أجل
$\displaystyle{\displaylines{s = 1}}$ حيث أثبتها
Von Mongoldt سنة 1897.
دالة
Mertens ضرورية جدا في محاولة إثبات
فرضية ريمان, حيث أنها
تكافئ أن التكامل يتقارب من أجل
$\displaystyle{\displaylines{\Re(s) > \frac{1}{2}}}$ :
وذلك واضح لأنه لو كانت دالة زيتا تقبل أصفارا في
$\displaystyle{\displaylines{ \frac{1}{2} < \Re(s) < 1}}$ فإن ذلك يعني أقطابا بالنسبة للدالة
$\displaystyle{\displaylines{s \rightarrow \dfrac{1}{\zeta(s)}}}$ وهو ما يعني تباعدا للتكامل
$\displaystyle{\displaylines{s \rightarrow \int_{1}^{+ \infty} \dfrac{M(x)}{x^{s+1}} dx}}$.
وعكسيا فإن تقارب التكامل من أجل
$\displaystyle{\displaylines{\dfrac{1}{2} < \Re(s) < 1}}$ يعني غيابا للأصفار بالنسبة لدالة
$\displaystyle{\displaylines{\zeta}}$ في
$\displaystyle{\displaylines{\dfrac{1}{2} < \Re(s) < 1}}$ وهو ما يثبت
فرضية ريمان.
كل ما هو مطلوب هو إيجاد دالة
$\displaystyle{\displaylines{f}}$ قابلة للتكامل بجوار
$\displaystyle{\displaylines{+ \infty}}$ تحقق العلاقة :
$\displaystyle{\displaylines{\left| \dfrac{M(x)}{x^{s+1}} \right| = \dfrac{|M(x)|}{x^{t+1}} = O(f(x)) , \quad t=\Re(s) > \frac{1}{2}}}$
اعتمادا على جدول من
$\displaystyle{\displaylines{10000}}$ قيمة للدالة
$\displaystyle{\displaylines{M}}$, اعتقد
Mertens أن العلاقة التالية دائما صحيحا :
$\displaystyle{\displaylines{\forall n > 1 \quad |M(n)| < \sqrt{n}}}$
لاحظ أن هذه الحدسية إن صحت فهي تثبت
فرضية ريمان لأن
$\displaystyle{\displaylines{\left| \dfrac{M(x)}{x^{s+1}} \right| = O \left(\dfrac{1}{x^{t+\frac{1}{2}}} \right)}}$, ونعلم أن
$\displaystyle{\displaylines{x \rightarrow \dfrac{1}{x^{t+\frac{1}{2}}}}}$ قابلة للتكامل بجوار
$\displaystyle{\displaylines{+ \infty}}$ إذا كان
$\displaystyle{\displaylines{t > \frac{1}{2}}}$.
سنة 1885 ادعى
Stieltjes أنه يملك برهان على
حدسية Mertens دون أن يقوم بنشره.
سنة 1985 استطاع كل من
Andrew Odlyzko و
Herman te Riele من إثبات خطأ
حدسية Mertens عبر إثبات الآتي :
$\displaystyle{\displaylines{\lim_{x \rightarrow + \infty} \sup \frac{M(x)}{\sqrt{x}} > 1.06 , \quad \lim_{x \rightarrow + \infty} \inf \frac{M(x)}{\sqrt{x}} < - 1.009}}$
بل أثبتوا أيضا أن المتفاوتة
$\displaystyle{\displaylines{|M(x)| > \sqrt{x}}}$ تتحقق في مالانهاية من المرات !
لا نعرف حاليا قيمة رقمية للمثال المضاد الذي نعلم بوجوده, لكن نعلم أنه أصغر من
$\displaystyle{\displaylines{\exp(3.21 \times 10^{64}) \approx 10^{10^{65}}}}$, وهو رقم خيالي جدا لا يمكننا الوصول إليه لا من قريب ولا من بعيد حيث أكبر قيمة موجودة للدالة
$\displaystyle{\displaylines{M}}$ سنة 2016 هي من أجل
$\displaystyle{\displaylines{x = 10^{16}}}$.
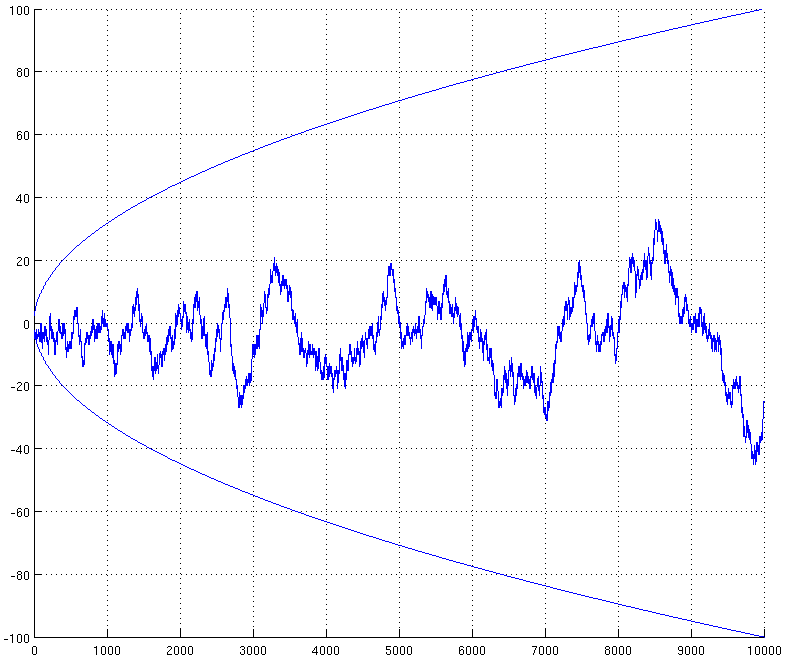
قيم الدالة M حتى x=10000.
ويظهر كيف أنها أصغر من جذر مربع لـx.
تم إثبات لاحقا خطأ هذه الحدسية.
على الرغم من خطأ
حدسية Mertens فإننا لا نعلم صحة
حدسية Mertens المعممة :
$\displaystyle{\displaylines{M(x) = O(\sqrt{x})}}$
وهو ما يعني وجود ثابتة
$\displaystyle{\displaylines{A}}$ تحقق الآتي انطلاقا من
$\displaystyle{\displaylines{x \geq x_0}}$ :
$\displaystyle{\displaylines{|M(x)| < A \sqrt{x}}}$
خطأ
حدسية Mertens يعني أنه من الضروري
$\displaystyle{\displaylines{A > 1}}$, لكن لحد الآن لا نعلم صحة
حدسية Mertens المعممة.
صحة
حدسية Mertens المعممة تثبت
فرضية ريمان.
لازلنا نجهل الكثير حول سلوك الدالة
$\displaystyle{\displaylines{M}}$, أقصى ما يمكننا إثباته هو اعتمادا على المنطقة بدون أصفار :
$\displaystyle{\displaylines{M(x) = O(x e^{- a \ln(x)^{3/5} \ln(\ln(x))^{-1/5}})}}$
محاولة لحل المعضلة, هناك صيغة ضعيفة من
حدسية Mertens المعممة :
$\displaystyle{\displaylines{\int_{1}^{x} \dfrac{M^{2}(u)}{u^2} du = O(\ln(x))}}$
حدسية Mertens المعممة تستلزم
حدسية Mertens المعممة الضعيفة, كما أن هذه الأخيرة تثبت
فرضية ريمان لكنها تبقى بدون حل أيضا.
فرضية ريمان تكافئ العبارة التالية :$\displaystyle{\displaylines{\forall \epsilon > 0 \quad M(x) = O(x^{\frac{1}{2} + \epsilon})}}$
عبارات تكافئ فرضية ريمان
استطاع علماء الرياضيات إيجاد الكثير من النتائج المكافئة لـ
فرضية ريمان, هذه النتائج إن تم إثبات إحداها صحيحة فستحل فرضية ريمان, لكنها تبقى أيضا عصية على الحل.
إن حل
فرضية ريمان يعني إثبات العديد من النتائج المهمة في الرياضيات, وهذه بعض العبارات المتكافئة مع فرضية ريمان :
 Von Koch 1901, فرضية ريمان تكافئ :
Von Koch 1901, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall \epsilon > 0, \qquad |\pi(x) - \text{Li}(x)| = O(x^{\frac{1}{2} + \epsilon})}}$
بحيث
$\displaystyle{\displaylines{\pi(x)}}$ تمثل دالة حساب عدد الأعداد الأولية الأصغر من
$\displaystyle{\displaylines{x}}$, و
$\displaystyle{\displaylines{\text{Li}(x) = \int_{2}^{x} \dfrac{dt}{\ln(t)}}}$ دالة تكامل اللوغاريتم.
وهو ما يكافئ أيضا :
$\displaystyle{\displaylines{\forall \epsilon > 0, \qquad p_n = \text{Li}^{-1}(n) + O(n^{\frac{1}{2} + \epsilon})}}$
بحيث
$\displaystyle{\displaylines{p_n}}$ العدد الأولي من الرتبة
$\displaystyle{\displaylines{n}}$, و
$\displaystyle{\displaylines{\text{Li}^{-1}}}$ الدالة العكسية للدالة
$\displaystyle{\displaylines{\text{Li}}}$.
 Littlewood 1912, فرضية ريمان تكافئ :
Littlewood 1912, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall \epsilon > 0, \qquad M(x) = O(x^{\frac{1}{2} + \epsilon})}}$
بحيث
$\displaystyle{\displaylines{M}}$ هي دالة
Mertens.
 Riesz 1916, فرضية ريمان تكافئ :
Riesz 1916, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall \epsilon > 0, \qquad \sum_{k=1}^{+\infty} \dfrac{(2k)!}{B_{2k} (k-1)!} x^{2 k} = O(x^{\frac{1}{2} + \epsilon})}}$
بحيث
$\displaystyle{\displaylines{B_{2k}}}$ تمثل أعداد برنولي.
 Speiser 1934, فرضية ريمان تكافئ :
Speiser 1934, فرضية ريمان تكافئ :الدالة $\displaystyle{\displaylines{\zeta^{'}}}$ ليس لها أصفار في المنطقة $\displaystyle{\displaylines{0 < \Re(s) < \frac{1}{2}}}$
 Schoenfeld 1976, فرضية ريمان تكافئ :
Schoenfeld 1976, فرضية ريمان تكافئ :$\displaystyle{\displaylines{|\pi(x) - \text{Li}(x)| = O(\sqrt{x} \ln(x))}}$
وبالضبط قام
Schoenfeld بإثبات التكافئ بين فرضية ريمان والمتفاوتة :
$\displaystyle{\displaylines{\forall x \geq 2756, \qquad |\pi(x) - \text{Li}(x)| \leq \frac{1}{8 \pi} \sqrt{x} \ln(x)}}$
 Robin 1984, فرضية ريمان تكافئ :
Robin 1984, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall n > 5040, \qquad \sigma(n) < e^{\gamma} n \ln(\ln(n))}}$
بحيث
$\displaystyle{\displaylines{\sigma(n)}}$ تمثل مجموع قواسم العدد
$\displaystyle{\displaylines{n}}$ و
$\displaystyle{\displaylines{\gamma}}$ ثابتة
Euler.
 Li 1997, فرضية ريمان تكافئ :
Li 1997, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall n \in \mathbb{N}, \qquad \dfrac{d^{n}}{dx^{n}} \left( s^{n} \ln\xi(s) \right)_{s = 1} \geq 0}}$
$\displaystyle{\displaylines{\xi(s) = \dfrac{1}{2} s (s-1) \pi^{-s/2} \Gamma(\dfrac{s}{2}) \zeta(s)}}$ Balazar, Saias, Yor 1999, فرضية ريمان تكافئ :
Balazar, Saias, Yor 1999, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\int_{- \infty}^{+ \infty} \ln\left|\zeta(\frac{1}{2}+it)\right| \frac{dt}{\frac{1}{4} + t^2} = 0}}$
 Lagarias 2002, فرضية ريمان تكافئ :
Lagarias 2002, فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall n \in \mathbb{N}^{*}, \qquad \sigma(n) \leq H_{n} + e^{H_{n}} \ln H_{n}}}$
بحيث
$\displaystyle{\displaylines{H_{n}}}$ تمثل المجموع المتناسق (
la somme Harmonique) :
$\displaystyle{\displaylines{H_{n} = \sum_{k=1}^{n} \frac{1}{k}}}$.
 Soundararajan 2009, فرضية ريمان تكافئ :
Soundararajan 2009, فرضية ريمان تكافئ :$\displaystyle{\displaylines{M(x) = O(\sqrt{x} \exp(\ln(x)^{1/2} \ln(\ln(x))^{14}))}}$
 فرضية ريمان تكافئ :
فرضية ريمان تكافئ :$\displaystyle{\displaylines{\forall n \geq 74 , \qquad 1 \vee 2 \vee \cdots \vee n \leq \exp(n + \frac{\sqrt{n} \ln(n)^2}{8 \pi})}}$
العلاقة مع الأعداد الأولية
الأعداد الأولية هي الأعداد الصحيحة الطبيعية التي لا تقبل القسمة إلا على نفسها وعلى
$\displaystyle{\displaylines{1}}$ (
راجع الأعداد الأولية).
البرهان على لا نهائية مجموعة الأعداد الأولية قديم ويعود إلى عالم الرياضي اليوناني
أقليدس الذي ولد سنة 300 قبل الميلاد..
إن غموض وتوزيع الأعداد الأولية الذي يظهر كما لو أنه عشوائي, ما زال موضوع بحث من طرف العلماء حتى الآن, وليس غريبا أن تكون الأعداد الأولية في صلب أغلب المسائل المفتوحة اليوم.
وتعتبر دالة
$\displaystyle{\displaylines{\zeta}}$ الفرصة لمحاولة فهم هذا التوزيع للأعداد الأولية داخل الأعداد الصحيحة الطبيعية.
كما رأينا سابقا فقد استطاع
Euler سنة 1737 من إثبات العلاقة التالية :
$\displaystyle{\displaylines{\zeta(x) = \prod_{\text{p premier}} \frac{1}{1 - p^{-x}} , \quad x > 1}}$
كما نعلم فدالة
$\displaystyle{\displaylines{\zeta}}$ تتباعد من أجل
$\displaystyle{\displaylines{x=1}}$, لدينا :
$\displaystyle{\displaylines{\sum_{k=1}^{+\infty} \frac{1}{k} = \prod_{\text{p premier}} \frac{p}{p-1} = \infty}}$
وبالتالي فإن تباعد دالة
$\displaystyle{\displaylines{\zeta}}$ في
$\displaystyle{\displaylines{x=1}}$ يستلزم أن مجموعة الأعداد الأولية غير منتهية.
جداء
Euler لدالة
$\displaystyle{\displaylines{\zeta}}$ مكنه من إثبات الآتي :
$\displaystyle{\displaylines{\sum_{\text{p premier}} \frac{1}{p} = \frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\cdots= \infty}}$
وبالضبط فقد بين أن :
$\displaystyle{\displaylines{\ln(\ln(n)) \leq \sum_{\substack{p \leq n \\ \text{p premier}}}\dfrac{1}{p} \leq \ln(\ln(n))+1}}$
العلاقة أعلاه تعني أن مجموع مقلوب الأعداد الأولية يتصرف مثل
$\displaystyle{\displaylines{\ln(\ln(n))}}$ في مالانهاية, وهي نتيجة رائعة بعد قرون من الجمود..
نعرف دالة حساب الأعداد الأولية الأصغر من
$\displaystyle{\displaylines{x}}$ كالآتي :
$\displaystyle{\displaylines{\pi :\begin{array}{rcl}\mathbb{R}_{+} & \rightarrow & \mathbb{N} \\ \\x & \rightarrow & \displaystyle\sum_{\substack{p \leq x \\ \text{p premier}}} 1 \end{array}}}$
$\displaystyle{\displaylines{\pi(x)}}$ تمثل عدد الأعداد الأولية الأصغر من
$\displaystyle{\displaylines{x}}$,
مثال : $\displaystyle{\displaylines{\pi(11,64) = \pi(11) = 5}}$في سن 15 سنة وبالإعتماد على جداول لقيم الأعداد الأولية واللوغاريتم الطبيعي, استطاع
Gauss أن يحدس سنة 1792 أن احتمال كون
$\displaystyle{\displaylines{n}}$ عدد أولي يقارب القيمة
$\displaystyle{\displaylines{\frac{1}{\ln(n)}}}$.
نحن نعلم أن احتمال كون
$\displaystyle{\displaylines{n}}$ عدد أولي هو
$\displaystyle{\displaylines{\frac{\pi(n)}{n}}}$, حدسية
Gauss تعني أنه
$\displaystyle{\displaylines{\frac{\pi(n)}{n} \approx \frac{1}{\ln(n)}}}$ أو على الأقل
$\displaystyle{\displaylines{\frac{\pi(n)}{n} \sim \frac{1}{\ln(n)}}}$.
لاحظ أن الكتابة
$\displaystyle{\displaylines{a_n \sim b_n}}$ تعني :
$\displaystyle{\displaylines{\lim_{n \rightarrow +\infty} \dfrac{a_{n}}{b_{n}} = 1}}$هذه الحدسية مكنت
Gauss من الآتي
$\displaystyle{\displaylines{\pi(x) \sim \int_{2}^{x} \frac{dt}{\ln(t)} = \text{Li}(x)}}$.
Gauss لم يستطع إثبات تخميناته, وهذه الدالة كانت محط اهتمام عالم آخر أيضا في نفس الوقت :
Legendre.
سنة 1808 اقترح
Legendre أن
$\displaystyle{\displaylines{\pi(n)}}$ تقارب
$\displaystyle{\displaylines{\frac{n}{\ln(n)+C}}}$ بحيث
$\displaystyle{\displaylines{C}}$ ثابتة وضعها
Legendre :
$\displaystyle{\displaylines{C = 1,08366}}$ لكن دون إثبات هذه العلاقة..
سنة 1852 أثبت العالم الروسي
Chebyshev المتفاوتة التالية من أجل
$\displaystyle{\displaylines{x \geq 30}}$ :
$\displaystyle{\displaylines{0,92 \frac{x}{\ln(x)} < \pi(x) < 1,11 \frac{x}{\ln(x)}}}$
سنة 1858 استطاع
Chebyshev من إثبات العلاقة :
$\displaystyle{\displaylines{\lim_{x \rightarrow + \infty} \inf \frac{\pi(x)}{x/\ln(x)} \leq 1 \leq \lim_{x \rightarrow + \infty} \sup \frac{\pi(x)}{x/\ln(x)}}}$
هذه العلاقة تثبت أن النسبة
$\displaystyle{\displaylines{\frac{\pi(x)}{x/\ln(x)}}}$ إذا كانت تقبل نهاية في
$\displaystyle{\displaylines{+\infty}}$ فهي
$\displaystyle{\displaylines{1}}$ : المشكل في إثبات وجود النهاية.
استطاع
Riemann لاحقا من إدخال طرق جديدة كليا عبر دراسة الدالة
$\displaystyle{\displaylines{\zeta}}$ لمتغير عقدي, وقام باكتشاف صيغة الدالة
$\displaystyle{\displaylines{\pi}}$ بدلالة الأصفار الغير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$.
لتكن
$\displaystyle{\displaylines{f(x)}}$ عدد الأعداد الأصغر من
$\displaystyle{\displaylines{x}}$ والتي تكتب على شكل
$\displaystyle{\displaylines{p^k}}$ بحيث
$\displaystyle{\displaylines{p}}$ عدد أولي, استطاع
Riemann إثبات الآتي :
$\displaystyle{\displaylines{f(x) = \text{li}(x) - \sum_{\rho} \text{li}(x^{\rho}) - \ln(2) + \int_{x}^{+\infty} \frac{du}{u (u^2 - 1) \ln(u)}}}$
بحيث المجموع على الأصفار الغير بديهية للدالة زيتا :
$\displaystyle{\displaylines{\zeta(\rho) = 0 \quad 0 < \Re(\rho) < 1}}$, و
$\displaystyle{\displaylines{x \rightarrow \text{li}(x) = \int_{0}^{x} \frac{dt}{\ln(t)}}}$ تمتل دالة تكامل اللوغاريتم .
هناك علاقة بين
$\displaystyle{\displaylines{f(x)}}$ و
$\displaystyle{\displaylines{\pi(x)}}$ لدينا :
$\displaystyle{\displaylines{\pi(x) = \sum_{n=1}^{+\infty} \frac{\mu(n)}{n} f(x^{\frac{1}{n}})}}$
بحيث
$\displaystyle{\displaylines{\mu}}$ تمثل دالة
Möbius التي رأيناها سابقا.
وبالتالي فإنه لدينا :
$\displaystyle{\displaylines{\pi(x) = R(x) - \sum_{\rho} R(x^{\rho})}}$
بحيث
$\displaystyle{\displaylines{x \rightarrow R(x) = \sum_{n=1}^{+\infty} \frac{\mu(n)}{n} \text{li}(x^{\frac{1}{n}})}}$ تمثل دالة
Riemann, والمجموع الثاني يتم على مجموعة الأصفار الغير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$.
صيغة
Reiman التي تجمع بين دالة حساب عدد الأعداد الأولية الأصغر من
$\displaystyle{\displaylines{x}}$ والأصفار الغير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$ تثبت الإرتباط الوثيق لهذه الدالة مع الأعداد الأولية وأن فهمنا لتوزيع هذه الأصفار سوف يمكننا من فهم توزيع الأعداد الأولية, لكن للأسف سرعان ما تعرض
Riemann لداء السل وتوفي مبكرا عن سن يناهز 39 سنة. وبالتالي لم يستطع
Riemann إكمال الطريق نحو حل التكافئ بين
$\displaystyle{\displaylines{\pi(x)}}$ و
$\displaystyle{\displaylines{\frac{x}{\ln(x)}}}$ لكن أعماله أحدثت تحولا كبيرا وطريقا زاخرا نحو مزيد من الإكتشافات كما سنرى لاحقا.
في سنة
1896 تمكن كل من
Hadamard و
de la Vallée Poussin من إثبات وبشكل مستقل أن الدالة
$\displaystyle{\displaylines{\zeta}}$ لا تنعدم من أجل
$\displaystyle{\displaylines{\Re(s)=1}}$, هذه الخاصية
تكافئ التالي :
$\displaystyle{\displaylines{\pi(x) \sim \frac{x}{\ln(x)}}}$
وهكذا تم إثبات حدسية
Gauss و
Legendre أو ما يسمى بـ
مبرهنة الأعداد الأولية.
وبما أن
$\displaystyle{\displaylines{\frac{x}{\ln(x)} \sim \text{Li}(x)}}$ فإنه لدينا
$\displaystyle{\displaylines{\pi(x) \sim \text{Li}(x)}}$.
مبرهنة الأعداد الأولية
تكافئ أيضا :
$\displaystyle{\displaylines{p_n \sim n \ln(n)}}$
بحيث
$\displaystyle{\displaylines{p_n}}$ يمثل العدد الأولي من الرتبة
$\displaystyle{\displaylines{n}}$.
الجدول التالي يقدم مختلف القيم الرقمية للدالة
$\displaystyle{\displaylines{\pi}}$ والدوال التي تحدثنا عليها سابقا :
| $\displaystyle{\displaylines{n}}$ | $\displaystyle{\displaylines{\pi(n)}}$ | $\displaystyle{\displaylines{\left|\pi(n) - \frac{n}{\ln(n)}\right|}}$ | $\displaystyle{\displaylines{\left| \pi(n) - \text{Li}(n)\right|}}$ | $\displaystyle{\displaylines{\left| \pi(n) - R(n) \right|}}$ |
| $\displaystyle{\displaylines{10^{8}}}$ | $\displaystyle{\displaylines{5\,761\,455}}$ | $\displaystyle{\displaylines{332\,774}}$ | $\displaystyle{\displaylines{754}}$ | $\displaystyle{\displaylines{97}}$ |
| $\displaystyle{\displaylines{10^{9}}}$ | $\displaystyle{\displaylines{50\,847\,534}}$ | $\displaystyle{\displaylines{2\,592\,592}}$ | $\displaystyle{\displaylines{1\,701}}$ | $\displaystyle{\displaylines{79}}$ |
| $\displaystyle{\displaylines{10^{10}}}$ | $\displaystyle{\displaylines{455\,052\,511}}$ | $\displaystyle{\displaylines{20\,758\,029}}$ | $\displaystyle{\displaylines{3\,104}}$ | $\displaystyle{\displaylines{1\,828}}$ |
| $\displaystyle{\displaylines{10^{11}}}$ | $\displaystyle{\displaylines{4\,118\,054\,813}}$ | $\displaystyle{\displaylines{169\,923\,159}}$ | $\displaystyle{\displaylines{11\,588}}$ | $\displaystyle{\displaylines{2\,318}}$ |
| $\displaystyle{\displaylines{10^{12}}}$ | $\displaystyle{\displaylines{37\,607\,912\,018}}$ | $\displaystyle{\displaylines{1\,416\,705\,193}}$ | $\displaystyle{\displaylines{38\,263}}$ | $\displaystyle{\displaylines{1\,476}}$ |
| $\displaystyle{\displaylines{10^{13}}}$ | $\displaystyle{\displaylines{346\,065\,536\,839}}$ | $\displaystyle{\displaylines{11\,992\,858\,452}}$ | $\displaystyle{\displaylines{108\,971}}$ | $\displaystyle{\displaylines{5\,773}}$ |
| $\displaystyle{\displaylines{10^{14}}}$ | $\displaystyle{\displaylines{3\,204\,941\,750\,802}}$ | $\displaystyle{\displaylines{102\,838\,308\,636}}$ | $\displaystyle{\displaylines{314\,890}}$ | $\displaystyle{\displaylines{19\,200}}$ |
كما بينا سابقا فإنه لدينا :
$\displaystyle{\displaylines{\lim_{x \rightarrow +\infty} \dfrac{\pi(x)}{\text{Li}(x)} = 1 \quad \lim_{x \rightarrow +\infty} \dfrac{\pi(x)}{x/\ln(x)} = 1 \quad \lim_{x \rightarrow +\infty} \dfrac{\pi(x)}{R(x)} = 1}}$

رسم الدالة pi (اللون الأحمر).
في الأعلى دالة تكامل اللوغاريتم Li
في الأسفر النسبة x/ln(x) .
لكن سرعة التقارب تختلف بين هذه الدوال ونرى من خلال الجدول كيف أن الدالة
$\displaystyle{\displaylines{\text{Li}}}$ تعتبر تقريب جيد للدالة
$\displaystyle{\displaylines{\pi}}$, والدالة
$\displaystyle{\displaylines{R}}$ أحسن بكثير, لكن سوف نقتصر على الدالة
$\displaystyle{\displaylines{\text{Li}}}$ لأنها سهلة في الحساب, بينما الدالة
$\displaystyle{\displaylines{R}}$ معقدة لإحتوائها على الدالة
$\displaystyle{\displaylines{\mu}}$ التي تتطلب معرفة قواسم العدد
$\displaystyle{\displaylines{n}}$ في كل تصاعد..
نحن نعرف الكثير حول تقريب
$\displaystyle{\displaylines{\frac{x}{\ln(x)}}}$ للدالة
$\displaystyle{\displaylines{\pi}}$ لكن نعرف القليل حول تقريب الدالة
$\displaystyle{\displaylines{\text{Li}}}$ لها.
رقميا اعتقد
Gauss أن العلاقة التالية دائما صحيحة :
$\displaystyle{\displaylines{\pi(x) \leq \text{Li}(x)}}$
سنة 1914 أثبت
Littlewood خطأ هذه المتفاوتة عبر إثباته أن
$\displaystyle{\displaylines{\pi(x) - \text{Li}(x)}}$ تغير الإشارة في مالانهاية من المرات!
سنة 1933 بين
S.Skewes أنه يوجد مثال يحقق
$\displaystyle{\displaylines{\pi(x) > \text{Li}(x)}}$ أصغر من
$\displaystyle{\displaylines{10^{10^{10^{34}}}}}$سنة 1987 قلص
H. te Riele هذا الرقم ليصل
$\displaystyle{\displaylines{10^{371} }}$, وهو بعيد جدا عن قدرة الحواسيب الحالية حيث أننا نعرف قيم
$\displaystyle{\displaylines{\pi(x)}}$ حتى
$\displaystyle{\displaylines{10^{20}}}$.
المتفاوتة السابقة تبين قوة البرهان الرياضي والحذر حول التعامل مع الفرضيات التي قد تبدو صحيحة لكن يتطلب إثباتها رياضيا للجزم بذلك.
الآن سوف نرى إلى أي مدى يمكننا تقريب القيمة
$\displaystyle{\displaylines{\pi(x)}}$ إلى
$\displaystyle{\displaylines{\text{Li}(x)}}$.
بدراسة دالة
$\displaystyle{\displaylines{\zeta}}$ يمكننا إثبات العلاقة التالية :
$\displaystyle{\displaylines{|\pi(x) - \text{Li}(x)| = O(x^{a} \ln(x))}}$
بحيث
$\displaystyle{\displaylines{a}}$ هو أكبر جزء حقيقي للأصفار الغير بديهية للدالة
$\displaystyle{\displaylines{\zeta}}$ :
$\displaystyle{\displaylines{a = \max \{ \Re(\rho) , \quad \zeta(\rho) = 0 \}}}$
نحن نعلم أن
$\displaystyle{\displaylines{0 < a < 1}}$ لكن تحت
فرضية ريمان فإننا نحصل على أحسن نتيجة لتقدير الخطأ بحيث سيكون لدينا
$\displaystyle{\displaylines{a = \frac{1}{2}}}$, بل إن فرضية ريمان تكافئ كما قلنا سابقا العبارة :
$\displaystyle{\displaylines{\forall x \geq 2756, \qquad |\pi(x) - \text{Li}(x)| \leq \frac{1}{8 \pi} \sqrt{x} \ln(x)}}$
إعتمادا على المنطقة بدون أصفار يمكننا إثبات العلاقة التالية :
$\displaystyle{\displaylines{|\pi(x) - \text{Li}(x)| = O(x \exp(-c \ln(x)^{3/5} \ln(\ln(x))^{-1/5} ))}}$
نتيجة المنطقة بدون أصفار مثبتة, لكن تبقى بعيدة عن النتائج المرجوة.
وبالتالي فإن حل
فرضية ريمان يعطي أحسن صيغة لتقريب الخطأ, لكن إلى أي مدى نسبة الخطأ التي تعطيها فرضية ريمان مقاربة للخطأ الفعلي ؟
تمكن
Littlewood من إثبات أن العلاقة التالية :
$\displaystyle{\displaylines{|\pi(x) - \text{Li}(x)| > c \sqrt{x} \dfrac{\ln(\ln(\ln(x)))}{\ln(x)}}}$
بحيث
$\displaystyle{\displaylines{c > 0}}$ ثابتة, تتحقق في ما لانهاية من المرات.
وهذا يعطينا فكرة أن المتفاوتة التي تحققها
$\displaystyle{\displaylines{|\pi(x) - \text{Li}(x)|}}$ تحت
فرضية ريمان هي في الحقيقة تقريب جيد لنسبة الخطأ.
بمعرفتنا الحالية, نحن نعلم مثلا أن
$\displaystyle{\displaylines{\pi(10^{100})}}$ قريب من
$\displaystyle{\displaylines{\text{Li}(10^{100}) = 4.3619 \times 10^{97}}}$ بنسبة خطأ أقصاها
$\displaystyle{\displaylines{\pm 0.03 \times 10^{97}}}$, وبالتالي فإننا متأكدون فقط من الرقمين الأوليين من قيمة
$\displaystyle{\displaylines{\pi(10^{100})}}$.
لكن تحت
فرضية ريمان فإن أقصى نسبة الخطأ تنخفض إلى
$\displaystyle{\displaylines{\pm 10^{51}}}$ ما يعني أننا متأكدون من
$\displaystyle{\displaylines{47}}$ رقم الأوائل لقيمة
$\displaystyle{\displaylines{\pi(10^{100})}}$.
قالوا عن فرضية ريمان
رغم العبارات المكافئة الكثيرة لـفرضية ريمان, إلا أنها ما زالت دون حل رغم المحاولات العديدة للكثير من العقول والنوابغ الذين أفنوا حياتهم في سبيل إيجادها تحل, وهذه بعض شهادات هئولاء العلماء :
 David Hilbert, واحد من أكبر الرياضيين في القرنين 19 و 20
David Hilbert, واحد من أكبر الرياضيين في القرنين 19 و 20 إذا قمت من نوم ألف سنة أول سؤال سأطرحه هل تم إثبات فرضية ريمان ؟
 Enrico Bombieri عالم رياضيات إيطالي ,حاصل على جائزة فيلدز سنة 1974
Enrico Bombieri عالم رياضيات إيطالي ,حاصل على جائزة فيلدز سنة 1974فرضية ريمان ليست فقط مشكلة : إنها المشكلة! وأهم مشكلة في الرياضيات.
إنها الإشارة إلى وجود شيء عميق وشامل في الرياضيات لم نصل بعد لفهمه.
 André Weil, واحد من أهم علماء الرياضيات في القرن العشرين
André Weil, واحد من أهم علماء الرياضيات في القرن العشرينعندما كنت صغيرا كنت أطمح أن أبين فرضية ريمان.
عندما أصبحت كبيرا قليلا كان لدي الأمل في أني أستطيع قراءة وفهم أحد براهين فرضية ريمان.
الآن أشك حتى في وجود إثبات عليها.





 إذا كان
إذا كان  إذا كان
إذا كان  إذا كان
إذا كان 

 إذا كان
إذا كان  إذا كان
إذا كان  إذا كان
إذا كان 




 Von Koch 1901, فرضية ريمان تكافئ :
Von Koch 1901, فرضية ريمان تكافئ : Littlewood 1912, فرضية ريمان تكافئ :
Littlewood 1912, فرضية ريمان تكافئ : Riesz 1916, فرضية ريمان تكافئ :
Riesz 1916, فرضية ريمان تكافئ : Speiser 1934, فرضية ريمان تكافئ :
Speiser 1934, فرضية ريمان تكافئ : Schoenfeld 1976, فرضية ريمان تكافئ :
Schoenfeld 1976, فرضية ريمان تكافئ : Robin 1984, فرضية ريمان تكافئ :
Robin 1984, فرضية ريمان تكافئ : Li 1997, فرضية ريمان تكافئ :
Li 1997, فرضية ريمان تكافئ : Balazar, Saias, Yor 1999, فرضية ريمان تكافئ :
Balazar, Saias, Yor 1999, فرضية ريمان تكافئ : Lagarias 2002, فرضية ريمان تكافئ :
Lagarias 2002, فرضية ريمان تكافئ : Soundararajan 2009, فرضية ريمان تكافئ :
Soundararajan 2009, فرضية ريمان تكافئ : فرضية ريمان تكافئ :
فرضية ريمان تكافئ :
 David Hilbert, واحد من أكبر الرياضيين في القرنين 19 و 20
David Hilbert, واحد من أكبر الرياضيين في القرنين 19 و 20  Enrico Bombieri عالم رياضيات إيطالي ,حاصل على جائزة فيلدز سنة 1974
Enrico Bombieri عالم رياضيات إيطالي ,حاصل على جائزة فيلدز سنة 1974 André Weil, واحد من أهم علماء الرياضيات في القرن العشرين
André Weil, واحد من أهم علماء الرياضيات في القرن العشرين