Un générateur de nombres aléatoires est un dispositif capable de produire une séquence de nombres aléatoires, notre but est de produire des suites
$\displaystyle{\displaylines{S}}$ de nombres aléatoires dans l'intervalle
$\displaystyle{\displaylines{]0,1[}}$$\displaystyle{\displaylines{S = \{a_0, a_1,\cdots,a_{n-1}\}}}$
Avec
$\displaystyle{\displaylines{\forall i \in \{0,1,\cdots,n-1\} \,\, : \,\, a_i \in ]0,1[}}$.
Les propriétés des nombres aléatoires:- Uniformément distribuées sur $\displaystyle{\displaylines{[0,1]}}$, c.-à-d ils sont équi-repartis sur $\displaystyle{\displaylines{[0,1]}}$
- Indépendants, c-à-d l'absence de tout lien déterministe entre ces nombres (la valeur $\displaystyle{\displaylines{a_i}}$ ne doit avoir aucune relation avec $\displaystyle{\displaylines{a_j}}$ tel que $\displaystyle{\displaylines{i \neq j}}$).
Définition: La suite
$\displaystyle{\displaylines{S = \{a_0, a_1,\cdots,a_{n-1}\}}}$ est uniformément distribuée sur
$\displaystyle{\displaylines{]0,1[}}$ ssi
$\displaystyle{\displaylines{\forall [\alpha, \beta[ \subset ]0,1[ \quad \frac{1}{n} \text{Card}\bigg[ \{a_0, a_1,\cdots,a_{n-1}\} \cap [\alpha, \beta[ \bigg] \approx \beta - \alpha}}$Le nombre
$\displaystyle{\displaylines{d=\beta - \alpha}}$ représente le diamètre de l'intervalle
$\displaystyle{\displaylines{[\alpha, \beta[}}$.
Par la définition, plus le diamètre
$\displaystyle{\displaylines{d}}$ est grand, plus la présence des nombres de la suite
$\displaystyle{\displaylines{S}}$ dans cet intervalle est importante.
Une suite de nombres aléatoires ne comporte pas des valeurs périodiques ou des valeurs très proches.
Avant L'apparition de l'ordinateur, la génération des suites de nombres aléatoires est réalisée par des méthodes physiques qui profitent du caractère aléatoire de certains phénomènes naturel qui semblent aléatoires.
Après l'apparition de l'ordinateur, la génération de nombres aléatoires se réalise par des méthodes itératives basé sur des algorithmes.
Un algorithme est une suite d'opérations prédéfinies que l'on applique à des paramètres pour les modifier. Si l'on applique le même traitement aux mêmes paramètres, les résultats sont donc identiques. En ce sens, un algorithme est donc
déterministe, à l'opposé de ce que l'on veut obtenir. Les nombres obtenus sont donc appelés
pseudo-aléatoiresGénérateur pseudo-aléatoire
Soit
$\displaystyle{\displaylines{f}}$ une fonction définit par :
$\displaystyle{\displaylines{f:\begin{array}{rcl}]0,1[ & \rightarrow & ]0,1[ \\x & \rightarrow & f(x) \end{array}}}$
Définition: un générateur pseudo-aléatoire est un algorithme qui génère à partir d'une valeur initiale
$\displaystyle{\displaylines{x_0}}$ une séquence de nombres pseudo-aléatoire.
$\displaystyle{\displaylines{G = \{ x_0, f(x_0), f^2(x_0), \cdots, f^{n-1}(x_0) \}}}$
$\displaystyle{\displaylines{f^k(x_0) = (f \circ f \circ \cdots \circ f)(x_0)}}$ $\displaystyle{\displaylines{k}}$ fois.
Dans la séquence
$\displaystyle{\displaylines{G}}$ nous voyons le lien déterministe entre
$\displaystyle{\displaylines{a_0 = x_0}}$ et
$\displaystyle{\displaylines{a_1 = f(x_0) \,\cdots}}$ c'est pourquoi on appelle
$\displaystyle{\displaylines{G}}$ générateur
pseudo-aléatoire.
Générateur de Von-Newmann
Le générateur de Von-Newmann est un générateur pseudo-aléatoire qui consiste à prendre un nombre et l’élever au carré et à prendre les chiffres au milieu comme sortie.
Exemple: $\displaystyle{\displaylines{x_0 = 787, \quad x_0^2 = 619369}}$
$\displaystyle{\displaylines{x_1 = 193, \quad x_1^2 = 37249}}$
$\displaystyle{\displaylines{x_2 = 372 \cdots}}$
Cette méthode est faible, et donne des séquences périodiques ou nulles à partir d'un certain rang, elle est remplacée en 1952 par Les générateurs congruentiels.
Générateur congruentiel
On définit la fonction
$\displaystyle{\displaylines{F}}$ d'un générateur congruentiel par:
$\displaystyle{\displaylines{F(x) = ax+b \mod m}}$
Propriétés :- $\displaystyle{\displaylines{F}}$ est une fonction périodique de periode $\displaystyle{\displaylines{T \leq m}}$.
- $\displaystyle{\displaylines{\forall n \in \mathbb{N}^{*} \quad 1 \leq F(x) \leq m-1}}$
- Pour $\displaystyle{\displaylines{f(x) =\frac{F(x)}{m}}}$, $\displaystyle{\displaylines{f(x) \in ]0,1[}}$
Pour générer la suite de nombre pseudo-aléatoire, on commence par un nombre aléatoire
$\displaystyle{\displaylines{x_0}}$ et on remplie notre suite par application à chaque fois la fonction
$\displaystyle{\displaylines{F}}$.
La taille
$\displaystyle{\displaylines{N}}$ de la séquence doit être inférieur à la période
$\displaystyle{\displaylines{T}}$.
Fonctionnement du générateur congruentiel :Le générateur congruentiel construit les nombres par application de la fonction
$\displaystyle{\displaylines{F}}$ déjà vu :
$\displaystyle{\displaylines{F(x) = ax+b \mod m}}$.
$\displaystyle{\displaylines{x_0, \, x_1=F(x_0) ,\, x_2=F^2(x_0) , \cdots, x_{n-1} = F^{n-1}(x_0)}}$
Avec
$\displaystyle{\displaylines{x_0}}$ un nombre aléatoire.
Ou avec la notation des suites :
$\displaystyle{\displaylines{\left\{ \begin{array}{cl}x_n & = \ a \, x_{n-1} + b \mod m \\ \\x_0 & \, \ \,\end{array} \right.}}$
Dans les langages de programmation, on peut obtenir
$\displaystyle{\displaylines{x_0}}$ par la fonction
date(), puisque le moment de l’exécution du programme semble aléatoire.
Pour quoi ce générateur produit des nombres pseudo-aléatoires et uniformément distribués sur $\displaystyle{\displaylines{]0,m[}}$ ?Soit
$\displaystyle{\displaylines{p \in \{ 1,2,3,\cdots,m-1 \}}}$ :
$\displaystyle{\displaylines{n = p \mod m \iff p = n \mod m \iff \exists q \in \mathbb{N} \, : \,n = mq+p}}$
Puisque
$\displaystyle{\displaylines{1 \leq p \leq m-1}}$ on a
$\displaystyle{\displaylines{p}}$ est le reste de la division euclidienne de
$\displaystyle{\displaylines{n}}$ par
$\displaystyle{\displaylines{m}}$.
Le comportement aléatoire de
$\displaystyle{\displaylines{x_k = F^{k}(x_0) = a F^{k-1}(x_0) + b \mod m}}$ vient du faite qu'on ne sait pas la valeur du reste de la division euclidienne de
$\displaystyle{\displaylines{a F^{k-1}(x_0) + b}}$ par
$\displaystyle{\displaylines{m}}$ qu'après le calcule.
Pour
$\displaystyle{\displaylines{b_k = a F^{k-1}(x_0) + b}}$, deux cas se posent :
1)
$\displaystyle{\displaylines{1 \leq b_k \leq m-1}}$ dans ce cas on aura
$\displaystyle{\displaylines{x_k = b_k}}$.
2)
$\displaystyle{\displaylines{m < b_k}}$ dans ce cas
$\displaystyle{\displaylines{b_k = p}}$ tel que
$\displaystyle{\displaylines{p}}$ est le reste de la division euclidienne de
$\displaystyle{\displaylines{b_k}}$ par
$\displaystyle{\displaylines{m}}$.
On voit donc les nombres oscillent dans
$\displaystyle{\displaylines{]0,m[}}$ et prennent toutes les valeurs possibles dans cet intervalle.
Qualité du genérateur :Le but du générateur est de construire des suites de nombres pseudo-aléatoires de taille 1000,10000 ...
Puisque La période
$\displaystyle{\displaylines{T}}$ de la fonction
$\displaystyle{\displaylines{F}}$ est inférieure à
$\displaystyle{\displaylines{m}}$, le nombre
$\displaystyle{\displaylines{m}}$ donc doit être très grand pour s'éloigner de cette périodicité.
Un bon générateur est celui qui a une période
$\displaystyle{\displaylines{T}}$ grande, pour cela on doit faire un bon chois sur les valeurs de
$\displaystyle{\displaylines{a}}$ et
$\displaystyle{\displaylines{b}}$.
Des études mathématiques prouve que la période peut atteindre
$\displaystyle{\displaylines{m}}$ pour certaines conditions sur
$\displaystyle{\displaylines{a}}$.
Exemple: Générateur de Lehmer:Le générateur de Lehmer est un générateur congruentiel avec
$\displaystyle{\displaylines{m=2^{31} - 1}}$ et
$\displaystyle{\displaylines{a=23}}$ et
$\displaystyle{\displaylines{b=0}}$.
La période
$\displaystyle{\displaylines{T}}$ de ce générateur est
$\displaystyle{\displaylines{T=\frac{m-1}{2} = 2^{30}-1 = 1073741823}}$Pseudo-code du générateur de Lehmer :
CODE:
Fonction suiteAleatoire(nombre n): nombre
nombre m ← 2^31 - 1,
a ← 23,
u ← Random(), // Nombre aléatoire dans [0,1]
x ← partieEtière((m-1)*u)+1,
i, suite[1..n];
Pour i de 1 à n Faire:
suite[i] ← x;
x ← a*x%m;
FinPour;
retourner suite;
FinFonction;
Méthode de Monte-Carlo pour approcher une intégrale
La méthode monté Carlo est une application de la génération des nombres aléatoires, elle donne une valeur approché de la valeur numérique de l'intégrale sur
$\displaystyle{\displaylines{[0,1]}}$ d'une fonction
$\displaystyle{\displaylines{g}}$ :
soit
$\displaystyle{\displaylines{g}}$ une fonction continue sur l'intervalle
$\displaystyle{\displaylines{[0,1]}}$, tel que :
$\displaystyle{\displaylines{I = \int_{0}^{1} g(x) dx}}$
Soit
$\displaystyle{\displaylines{U}}$ une variable aléatoire suit la loi Uniforme sur
$\displaystyle{\displaylines{[0,1]}}$.
Alors on a
$\displaystyle{\displaylines{E(g(U)) = \int_{\mathbb{R}} g(x) f_{U}(x) dx}}$, tel que
$\displaystyle{\displaylines{f_U}}$ est la fonction densité de la loi
$\displaystyle{\displaylines{U(0,1)}}$.
on a
$\displaystyle{\displaylines{f_U(x) = \left\{ \begin{array}{cl}1 & si \ x \in [0,1] \\0 & sinon \ \,\end{array} \right.}}$Donc on a
$\displaystyle{\displaylines{E(g(U)) = \int_{[0,1]} g(x) dx = I}}$.
Moyenne empirique:soit
$\displaystyle{\displaylines{X_1,X_2,\cdots,X_n}}$ des variables aléatoires indépendants et identiquement distribués (ont une Espérence
$\displaystyle{\displaylines{\mu}}$ et une variance
$\displaystyle{\displaylines{\sigma^2}}$).
La moyenne empirique est définit par
$\displaystyle{\displaylines{\overline{X}_{n} = \frac{1}{n} \sum_{k=1}^{n} X_k}}$ (On a
$\displaystyle{\displaylines{E(\overline{X}_{n}) = \mu}}$)
La
loi faible des grands nombres annonce que
$\displaystyle{\displaylines{\overline{X}_{n}}}$ converge en probabilité vers
$\displaystyle{\displaylines{\mu}}$.
$\displaystyle{\displaylines{\overline{X}_{n} \rightarrow_{n \rightarrow +\infty}^{Pr} \mu}}$
En d'autre terme :
$\displaystyle{\displaylines{\forall \epsilon > 0, \quad \lim_{n \rightarrow + \infty} P(|\overline{X}_{n} - \mu| > \epsilon ) = 0}}$
On sait que
$\displaystyle{\displaylines{P(|\overline{X}_{n} - \mu| > \epsilon ) + P(|\overline{X}_{n} - \mu| \leq \epsilon ) = 1}}$, donc:
$\displaystyle{\displaylines{\forall \epsilon > 0, \quad \lim_{n \rightarrow + \infty} P(|\overline{X}_{n} - \mu| \leq \epsilon ) = 1}}$
Pour un
$\displaystyle{\displaylines{n}}$ trés grand et
$\displaystyle{\displaylines{\epsilon}}$ trop petit on aura :
$\displaystyle{\displaylines{P(|\overline{X}_{n} - \mu| \leq \epsilon ) \approx 1}}$Donc on a
fort probable que
$\displaystyle{\displaylines{|\overline{X}_{n} - \mu| \leq \epsilon}}$ ou encore, on a fort probable que la différence
$\displaystyle{\displaylines{|\overline{X}_{n} - \mu|}}$ est trop petite.
Donc on a $\displaystyle{\displaylines{\overline{X}_{n} \approx \mu}}$
Pour
$\displaystyle{\displaylines{U_1,U_2,U_3,\cdots,U_n}}$ des variables aléatoires indépendantes et identiquement distribuées de la loi
$\displaystyle{\displaylines{U(0,1)}}$ on a :
$\displaystyle{\displaylines{g(U_1),g(U_2),g(U_3),\cdots,g(U_n)}}$ des V.A i.i.d. D’où pour
$\displaystyle{\displaylines{n}}$ un nombre trés grand on a :
$\displaystyle{\displaylines{\frac{1}{n} \sum_{k=1}^{n} g(U_k) \approx E(g(U_1)) \approx I}}$
On peut donc évaluer la valeur Numérique de l'intégrale
$\displaystyle{\displaylines{I = \int_{0}^{1} g(x) dx}}$ par cette approche probabiliste.
La valeur numérique donnée par
$\displaystyle{\displaylines{\frac{1}{n} \sum_{k=1}^{n} g(U_k)}}$ reste une approximation, et on a aucune garentie sur sa précision.
Pour
$\displaystyle{\displaylines{x_1,x_2,\cdots,x_{n}}}$ des nombres aléatoires dans
$\displaystyle{\displaylines{[0,1]}}$ on a :
$\displaystyle{\displaylines{\frac{1}{n} \sum_{k=1}^{n} g(x_k) \approx \int_{0}^{1} g(x) dx}}$
On peut donc écrire un pseudo-code qui donne une approximation de la valeur de l'intégrale
$\displaystyle{\displaylines{I}}$ par la méthode de Monte-Carlo.
CODE:
Fonction MonteCarlo(nombre n):nombre
nombre s ← 0,
suite[1..n], i;
suite ← suiteAleatoire(n);
Pour i ← 1 à n Faire:
s ← s + g(suite[i]);
FinPour;
s ← s / n;
retourner s;
FinFonction
Pour
$\displaystyle{\displaylines{-\infty < a < b < +\infty}}$, soit
$\displaystyle{\displaylines{g}}$ une fonction continue sur
$\displaystyle{\displaylines{[a,b]}}$, et soit :
$\displaystyle{\displaylines{I=\int_{a}^{b} g(t) dt}}$
Effectuons le changement de variable :
$\displaystyle{\displaylines{u = \frac{t-a}{b-a}}}$, on a :
$\displaystyle{\displaylines{I = (b-a) \int_{0}^{1} f((b-a) u + a) du}}$
Soit
$\displaystyle{\displaylines{g}}$ une fonction continue et intégrable sur
$\displaystyle{\displaylines{[a,+\infty[}}$ (
$\displaystyle{\displaylines{a \neq -1}}$), et soit:
$\displaystyle{\displaylines{I=\int_{a}^{+\infty} g(t) dt}}$
Effectuons le changement de variable :
$\displaystyle{\displaylines{u = \frac{a+1}{t+1}}}$, on a :
$\displaystyle{\displaylines{I = (a+1) \int_{0}^{1} g\left(\frac{a+1}{u}-1\right) \frac{du}{u^2}}}$
Intégrale multiple:Soit
$\displaystyle{\displaylines{g}}$ une fonction de
$\displaystyle{\displaylines{p}}$ variables, continue sur
$\displaystyle{\displaylines{[0,1]\times[0,1]\times\cdots\times [0,1]}}$, et soit
$\displaystyle{\displaylines{I}}$ :
$\displaystyle{\displaylines{I = \int_{0}^{1}\int_{0}^{1} \cdots \int_{0}^{1} g(x_1,x_2,\cdots,x_p) dx_1 \, dx_2 \cdots dx_p}}$
soit
$\displaystyle{\displaylines{U_1,U_2,\cdots,U_p}}$ des variables aléatoires indépendants et identiquement distribuées de la loi
$\displaystyle{\displaylines{U(0,1)}}$.
On a :
$\displaystyle{\displaylines{I = E(g(U_1,U_2,\cdots,U_p))}}$
Pour
$\displaystyle{\displaylines{n}}$ un nombre très grand, on a :
$\displaystyle{\displaylines{\frac{1}{n} \sum_{k=1}^{n} g(U_{1,k},U_{2,k},\cdots,U_{p,k}) \approx I}}$
Avec
$\displaystyle{\displaylines{U_{1,k},U_{2,k},\cdots,U_{p,k}}}$ pour
$\displaystyle{\displaylines{k\in\{1,2,\cdots,n\}}}$ des variables aléatoires indépendants et identiquement distribuées de la loi
$\displaystyle{\displaylines{U(0,1)}}$.
Définition: la simulation de façon générale est l'imitation d'un phénomène dans le domaine numérique, exemple: les simulateurs de pilotage d'avion ...
Définition: la simulation d'une variable aléatoire
$\displaystyle{\displaylines{X}}$ consiste à fabriquer une variable aléatoire
$\displaystyle{\displaylines{X_1}}$ de telle façon
$\displaystyle{\displaylines{X_1}}$ simule
$\displaystyle{\displaylines{X}}$, c-à-d
$\displaystyle{\displaylines{X_1}}$ joue le même rôle de
$\displaystyle{\displaylines{X}}$ dans le monde numérique.
Exemple: une usine fabrique des batteries.
La probabilité qu'une batterie soit défectueuse est
$\displaystyle{\displaylines{10\%}}$.
Soit
$\displaystyle{\displaylines{X}}$ la variable aléatoire : "état d'une batterie" :
Pour une batterie donnée, soit elle est en bonne état
$\displaystyle{\displaylines{X=1}}$, soit elle est défectueuse
$\displaystyle{\displaylines{X=0}}$.
Représentons la situation dans un tableaux :
| $\displaystyle{\displaylines{X}}$ | $\displaystyle{\displaylines{0}}$ | $\displaystyle{\displaylines{1}}$ |
| $\displaystyle{\displaylines{P(X=k)}}$ | $\displaystyle{\displaylines{0.1}}$ | $\displaystyle{\displaylines{0.9}}$ |
Écrivons un pseudo-code qui simule cette situation, c-à-d un algorithme qui "prend" une batterie artificielle et nous renvois l'état de cette batterie :
CODE:
nombre etat;
u ← Random(); // Nombre aléatoire dans [0,1]
Si u <= 0.9 Alors:
etat ← 1;
Sinon
etat ← 0;
FinSi;
Afficher(etat);

Fonctionnement de l'algorithme
Dans notre algorithme on teste la valeur du nombre aléatoire u, c'est ça place qui décide l'état de la batterie artificielle, nous verrons dans le chapitre suivant que cette méthode s'appelle
la transformation inverse.
Soit
$\displaystyle{\displaylines{X}}$ une variable aléatoire discrète fini, tel que:
$\displaystyle{\displaylines{X(\Omega) = \{x_1,x_2,\cdots,x_n\} \, , \, P(X=x_i) = p_i \quad \forall i=1,2,\cdots,n}}$
Définition d'un simulateur:On dit que
$\displaystyle{\displaylines{X_1}}$ est un simulateur de
$\displaystyle{\displaylines{X}}$ si et seulement si :
- $\displaystyle{\displaylines{X(\Omega) = X_1(\Omega)}}$
- $\displaystyle{\displaylines{P(X_1=x_i) = P(X=x_i) \quad \forall i=1,2,\cdots,n}}$
La simulation de
$\displaystyle{\displaylines{X}}$ consiste à écrire le pseudo-code du simulateur
$\displaystyle{\displaylines{X_1}}$. Ce pseudo-code retourne une des valeurs de
$\displaystyle{\displaylines{X(\Omega)}}$ (le simulateur
$\displaystyle{\displaylines{X_1}}$ construit l'expérience et annonce le résultat obtenue
$\displaystyle{\displaylines{x_k \in X(\Omega)}}$ ).
Soit
$\displaystyle{\displaylines{X}}$ une variable aléatoire discrète fini :
$\displaystyle{\displaylines{X(\Omega) = \{x_0,x_1,\cdots, x_n\}}}$,
$\displaystyle{\displaylines{P(X = x_i) = p_i}}$ pour
$\displaystyle{\displaylines{i \in \{0,1,\cdots,n\}}}$.
Avec
$\displaystyle{\displaylines{x_0 < x_1 < x_2 < \cdots < x_n}}$ (choix organisationnel).
Soit
$\displaystyle{\displaylines{U}}$ une variable aléatoire qui suit la loi
$\displaystyle{\displaylines{U(0,1)}}$, et
$\displaystyle{\displaylines{X_1}}$ la variable aléatoire définit par :
$\displaystyle{\displaylines{X_1 = \left\{ \begin{array}{cl}x_0 & si \ 0 \leq U \leq p_0 \\x_1 & si \ p_0 < U \leq p_0 + p_1 \\\, & \vdots \ \, \\x_k & si \ p_0+p_1 + \cdots + p_{k-1} < U \leq p_0+p_1 + \cdots + p_{k} \\x_n & si \ p_0+p_1 + \cdots + p_{n-1} < U \leq 1\end{array} \right.}}$
Organisons les bornes des intervalles : soit
$\displaystyle{\displaylines{F_{X}}}$ la fonction de répartition de la loi
$\displaystyle{\displaylines{X}}$.
$\displaystyle{\displaylines{\begin{array}{rcl}F_{X}(x_k) & = & P(X \leq x_k) \\& = & \displaystyle\sum_{i=0}^{k} P(X = x_i) \\& = & \displaystyle\sum_{i=0}^{k} p_i \end{array}}}$
Donc,
$\displaystyle{\displaylines{X_1 = \left\{ \begin{array}{cl}x_0 & si \ 0 \leq U \leq F_{X}(x_0) \\x_1 & si \ F_{X}(x_0) < U \leq F_{X}(x_1) \\\, & \vdots \ \, \\x_k & si \ F_{X}(x_{k-1}) < U \leq F_{X}(x_k) \\x_n & si \ F_{X}(x_{n-1}) < U \leq 1\end{array} \right.}}$
Proposition: $\displaystyle{\displaylines{X_1}}$ est un simulateur de
$\displaystyle{\displaylines{X}}$, et cette méthode de simulation s'appelle
méthode de la transformation inverse.
Preuve:1) Il est claire que
$\displaystyle{\displaylines{X_1(\Omega) = X(\Omega)}}$.
2) Montrons que:
$\displaystyle{\displaylines{\forall k \in \{0,1,2,\cdots,n\} \quad P(X_1 = x_k) = P(X = x_k)}}$.
On a
$\displaystyle{\displaylines{\{X_1 = x_k\} = \{F_{X}(x_{k-1}) < U \leq F_{X}(x_k) \}}}$Donc,
$\displaystyle{\displaylines{ \begin{array}{rcl}P(X_1 = x_k) & = & P(F_{X}(x_{k-1}) < U \leq F_{X}(x_k) ) \\& = & F_{X}(x_k) - F_{X}(x_{k-1}) \quad (\star) \\& = & \displaystyle\sum_{i=0}^{k} P(X = x_i) - \displaystyle\sum_{i=0}^{k-1} P(X = x_i) \\& = & P(X = x_k)\end{array}}}$
Dans
$\displaystyle{\displaylines{(\star)}}$ il suffit de voir que
$\displaystyle{\displaylines{U}}$ est une V.A qui suit
$\displaystyle{\displaylines{U(0,1)}}$, Donc
$\displaystyle{\displaylines{P(a < U \leq b) = \int_{a}^{b} f_{U}(t) dt}}$ avec
$\displaystyle{\displaylines{f_U}}$ fonction densité de
$\displaystyle{\displaylines{U}}$ :
$\displaystyle{\displaylines{f_U(t) = \left\{ \begin{array}{cl}1 & si \ t \in [0,1] \\0 & sinon \ \,\end{array} \right.}}$
Si
$\displaystyle{\displaylines{0 \leq a < b \leq 1}}$ on a
$\displaystyle{\displaylines{P(a < U \leq b) = \int_{a}^{b} 1 \, dt = b-a}}$ et c'est le cas dans
$\displaystyle{\displaylines{(\star)}}$ puisque
$\displaystyle{\displaylines{\forall x \in \mathbb{R} \quad : \, 0 \leq F_X(x) \leq 1}}$ (
$\displaystyle{\displaylines{F_X(x) = P(X \leq x)}}$).
Résultat: $\displaystyle{\displaylines{X1}}$ est un simulateur de
$\displaystyle{\displaylines{X}}$.
Pseudo-Code de la tansformation Inverse :CODE:
Fonction TransformationInverse(nombre X[1..n], nombre P[1..n]):nombre
nombre F ← 0,
i ← 1,
u ← Random(); // Nombre aléatoire dans [0,1]
Tant-Que F < u faire :
F ← F + P[i];
i ← i + 1;
FinTant-Que;
retourner X[i-1];
FinFonction;
Pour simuler une variable aléatoire discrète fini, il suffit de remplir les tableaux
X[1..n] et
P[1..n] par les valeurs de
$\displaystyle{\displaylines{X(\Omega)}}$ et
$\displaystyle{\displaylines{P(X=x_k)\, , k=1,2,\cdots,n}}$.
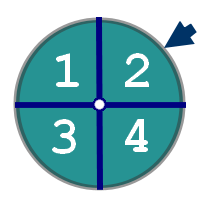
Exercice: Considérons une roue divisé en 4 parties, on tourne la roue et le résultat obtenue égale au chiffre opposé à la flèche.
Après plusieurs observations, nous obtenons les résultats suivants:
Les résultats 1,2,3,4 sont obtenues respectivement avec les probabilités :
$\displaystyle{\displaylines{\frac{2}{10},\,\frac{3}{10},\,\frac{1}{10},\,\frac{4}{10}}}$.
Soit
$\displaystyle{\displaylines{X}}$ la variable aléatoire : "résultat de la roue", on a
$\displaystyle{\displaylines{X(\Omega) = \{1,2,3,4\}}}$.
| $\displaystyle{\displaylines{X}}$ | $\displaystyle{\displaylines{1}}$ | $\displaystyle{\displaylines{2}}$ | $\displaystyle{\displaylines{3}}$ | $\displaystyle{\displaylines{4}}$ |
| $\displaystyle{\displaylines{P(X=k)}}$ | $\displaystyle{\displaylines{\frac{2}{10}}}$ | $\displaystyle{\displaylines{\frac{3}{10}}}$ | $\displaystyle{\displaylines{\frac{1}{10}}}$ | $\displaystyle{\displaylines{\frac{4}{10}}}$ |
1) On utilisant la Fonction
TransformationInverse(), Le pseudo-code du simulateur de la loi
$\displaystyle{\displaylines{X}}$ :
CODE:
Fonction Simulateur():nombre
nombre X[1..4], P[1..4];
X[1] ← 1;X[2] ← 2;X[3] ← 3;X[4] ← 4;
P[1] ← 2/10;P[2] ← 3/10;P[3] ← 1/10;P[4] ← 4/10;
retourner TransformationInverse(X, P);
FinFonction;
2) Pseudo-code on utilisant la transformation inverse directement :
CODE:
Fonction Simulateur():nombre
nombre u ← Random();
Si 0 =< u =< 2/10 Alors:
retourner 1;
FinSi;
Si 2/10 < u =< 5/10 Alors:
retourner 2;
FinSi;
Si 5/10 < u =< 6/10 Alors:
retourner 3;
FinSi;
Si 6/10 < u =< 1 Alors:
retourner 4;
FinSi;
FinFonction;
| $\displaystyle{\displaylines{X}}$ | $\displaystyle{\displaylines{0}}$ | $\displaystyle{\displaylines{1}}$ |
| $\displaystyle{\displaylines{P(X=k)}}$ | $\displaystyle{\displaylines{1-p}}$ | $\displaystyle{\displaylines{p}}$ |
Pseudo-code en utilisons la fonction
TransformationInverse.
CODE:
Fonction Bernoulli(nombre p):nombre
nombre X[1..2], P[1..2];
X[1] ← 0;
X[2] ← 1;
P[1] ← 1-p;
P[2] ← p;
retourner TransformationInverse(X, P);
FinFonction;
Pseudo-code on utilisons la méthode de la transformation inverse directement :
CODE:
Fonction Bernoulli(nombre p):nombre
nombre x,
u ← Random();
Si u < (1-p) Alors:
x ← 0;
Sinon
x ← 1;
FinSi;
retourner x;
FinFonction;
on utilisons le faite que
$\displaystyle{\displaylines{Y}}$ qui suit la loi binomiale de paramètre n et p est la somme de n variables aléatoires de Bernoulli de paramètre p :
$\displaystyle{\displaylines{Y = \sum_{i=1}^{n}B_i}}$ (Les
$\displaystyle{\displaylines{B_i}}$ sont indépendants et identiquement distribuées).
CODE:
Fonction Binomiale(nombre n, nombre p):nombre
nombre i, k ← 0;
Pour i ← 1 à n Faire:
k ← k + Bernoulli(p);
FinPour;
retourner k;
FinFonction;
Pseudo-code on utilisons la méthode de la transformation inverse directement :
On sait que la loi de probabilité de B(n,p) :
$\displaystyle{\displaylines{P(X=k) = C_{n}^{k} p^k (1-p)^{n-k}}}$.
On a :
$\displaystyle{\displaylines{\left\{ \begin{array}{cl}P(X=k+1) & = \ \dfrac{p}{1-p} \dfrac{n-k}{k+1} P(X=k) \\ \\P(X=0) & = \ (1-p)^n\end{array} \right.}}$
CODE:
Fonction Binomiale(nombre n, nombre p):nombre
nombre F ← 0,
k ← 0,
u ← Random(),
c ← p/(1-p),
q ← (1-p)^n;
Tant-Que F < u faire :
F ← F + q;
q ← c*(n-k)*q/(k+1);
k ← k + 1;
FinTant-Que;
retourner (k-1);
FinFonction;
Variables aléatoires discrètes fini et infini
La méthode de la transformation inverse reste vrai pour une variable aléatoire
$\displaystyle{\displaylines{X}}$ à domaine infini:
$\displaystyle{\displaylines{X_1 = \left\{ \begin{array}{cl}x_0 & si \ 0 \leq U \leq F_{X}(x_0) \\x_1 & si \ F_{X}(x_0) < U \leq F_{X}(x_1) \\\, & \vdots \ \, \\x_k & si \ F_{X}(x_{k-1}) < U \leq F_{X}(x_k) \\ \, & \vdots \ \,\end{array} \right.}}$
Pseudo-code du simulateur de la loi géométrique de paramètre p:La loi géométrique de paramètre
$\displaystyle{\displaylines{p}}$ est la probabilité d'avoir le premier succès lorsqu'on réalise des expériences indépendants chacune a pour probabilité de succès
$\displaystyle{\displaylines{p}}$ :
$\displaystyle{\displaylines{X(\Omega) = \{1,2,3,\cdots\} \quad P(X=k) = (1-p)^{k-1} p}}$
CODE:
Fonction Géométrique(nombre p):nombre
nombre F ← 0,
k ← 1,
u ← Random(), q;
Tant-Que F < u faire :
q ← (1-p)^(k-1)*p
F ← F + q;
k ← k + 1;
FinTant-Que;
retourner (k-1);
FinFonction;
L’exécution du programme risque d’être très lente si
$\displaystyle{\displaylines{u}}$ est trés proche de
$\displaystyle{\displaylines{1}}$ (très grandes itérations dans la boucle Tant-Que). Et pour
$\displaystyle{\displaylines{u=1}}$ la boucle sera infini.
Solution: soit
$\displaystyle{\displaylines{X}}$ une variable aléatoire discrète à domaine infini.
Puisque
$\displaystyle{\displaylines{P(X \leq x) + P(X > x) = 1}}$, on a :
$\displaystyle{\displaylines{F_{X}(x) = 1 - P(X > x)}}$
Soit
$\displaystyle{\displaylines{I_{N} = \{x \in X(\Omega) \, | \, X > N \}}}$.
On a :
$\displaystyle{\displaylines{F_{X}(N) = 1 - \sum_{x_i \in I_N} P(X = x_i)}}$
On sait que :
$\displaystyle{\displaylines{\lim_{x \rightarrow +\infty} F_{X}(x) = 1}}$
Donc Pour
$\displaystyle{\displaylines{N}}$ un nombre très grand :
$\displaystyle{\displaylines{\sum_{x_i \in I_N} P(X = x_i) \approx 0}}$Notre but est de déterminer le plus grand nombre N qui vérifie
$\displaystyle{\displaylines{F_{X}(N) < 1 - \epsilon}}$, avec
$\displaystyle{\displaylines{\epsilon > 0}}$ un nombre donné assez petit que l'on veut.
Donc on peut travailler sur l'intervalle
$\displaystyle{\displaylines{[1,N]}}$ et on restreint
$\displaystyle{\displaylines{X(\Omega)}}$ sur
$\displaystyle{\displaylines{\{x_1,x_2,\cdots,x_N\}}}$ puisque les événements
$\displaystyle{\displaylines{\{x_{N+1},x_{N+2},\cdots\}}}$ donnent des probabilité négligeables.
Simuler la Loi de Poisson de paramètre $\displaystyle{\displaylines{\lambda}}$ Avec $\displaystyle{\displaylines{\epsilon=0.0001}}$ :La loi de Poisson est définit par La loi :
$\displaystyle{\displaylines{P(X=k) = e^{-\lambda} \dfrac{\lambda^k}{k!}}}$ pour
$\displaystyle{\displaylines{k=0,1,2,\cdots}}$On a :
$\displaystyle{\displaylines{\left\{ \begin{array}{cl}P(X=k+1) & = \ \dfrac{\lambda}{k+1} P(X=k) \\P(X=0) & = \ e^{-\lambda}\end{array} \right.}}$
CODE:
Fonction Poisson(nombre lambda):nombre
nombre N, epsilon ← 0.0001,
q ← exp(-lambda),
F ← 0,
u ← Random(),
k ← 0;
Tant-Que F < (1 - epsilon) Faire:
F ← F + q;
q ← lambda * q / (k+1);
k ← k+1;
FinTant-Que;
N ← k-1;
k ← 0;
F ← 0;
q ← exp(-lambda);
Tant-Que F < u Faire:
F ← F + q;
Si k = N Alors:
F ← 1;
FinSi;
q ← lambda * q / (k+1);
k ← k+1;
FinTant-Que;
retourner (k-1);
FinFonction;
La condition suivante :
CODE:
Si k = N Alors:
F ← 1;
FinSi;
Est nécessaire pour ajouter l'intervalle perdu par l'élimination de l’événement
$\displaystyle{\displaylines{\{x_{N+1},x_{N+2},\cdots\}}}$ au dernier événement
$\displaystyle{\displaylines{\{x_N\}}}$.
Méthode de rejet-acceptation
Soit
$\displaystyle{\displaylines{X}}$ une variable aléatoire tel que
$\displaystyle{\displaylines{X(\Omega) = \{a_1,a_2,\cdots,a_n\}}}$, et
$\displaystyle{\displaylines{P(X = a_i) = p_i \quad \forall i=1,2,\cdots,n}}$.
Supposons qu'il existe une variable aléatoire
$\displaystyle{\displaylines{Y}}$ tel que :
- $\displaystyle{\displaylines{Y}}$ admet $\displaystyle{\displaylines{Y_1}}$ comme simulateur.
- $\displaystyle{\displaylines{Y(\Omega) = X(\Omega) = \{a_1,a_2,\cdots,a_n\}}}$, et $\displaystyle{\displaylines{P(Y = a_i) = q_i \quad \forall i=1,2,\cdots,n}}$.
- $\displaystyle{\displaylines{\forall i=1,2,\cdots,n \quad \frac{p_i}{q_i} \leq c}}$.
Soit
$\displaystyle{\displaylines{X_1}}$ la variable aléatoire définit par l'algorithme suivant :
- Soit $\displaystyle{\displaylines{a_k = Y_1}}$.
- Soit $\displaystyle{\displaylines{u}}$ un nombre aléatoire dans $\displaystyle{\displaylines{[0,1]}}$.
- Si $\displaystyle{\displaylines{u \leq \frac{p_k}{c \, q_k}}}$ Alors $\displaystyle{\displaylines{X_1 = a_k}}$, Sinon revenir à l'étape 2).
Proposition: $\displaystyle{\displaylines{X_1}}$ est un simulateur de
$\displaystyle{\displaylines{X}}$.
Preuve:1) il est claire que
$\displaystyle{\displaylines{X(\Omega) = X_1(\Omega)}}$.
2) Montrons que:
$\displaystyle{\displaylines{\forall i=1,2,\cdots,n \quad P(X_1=a_i) = P(X=a_i)}}$.
Dans la 3-éme étape de l'algorithme de la variable aléatoire
$\displaystyle{\displaylines{X_1}}$, deux cas se posent :
$\displaystyle{\displaylines{u \leq \frac{p_k}{c \, q_k}}}$ donc acceptation et
$\displaystyle{\displaylines{X_1 = a_k}}$ sinon rejet et refaire l'étape
2).
$\displaystyle{\displaylines{ \begin{array}{rcl}P(X_1 = a_i) & = & P(Y_1 = a_i \, / \, acceptation) \\ \\& = & \dfrac{P(\{Y_1 = a_i\} \, \text{et} \, \{acceptation\})}{P(acceptation)}\end{array}}}$
On a
$\displaystyle{\displaylines{\{Y_1 = a_i\} \, \text{et} \, \{acceptation\} = \{Y_1 = a_i\} \, \text{et} \, \{U \leq \frac{p_i}{c \, q_i}\}}}$.
Les événements
$\displaystyle{\displaylines{\{Y_1 = a_i\}}}$ et
$\displaystyle{\displaylines{\{U \leq \frac{p_i}{c \, q_i}\}}}$ sont indépendants, d’où
$\displaystyle{\displaylines{P(\{Y_1 = a_i\} \, \text{et} \, \{U \leq \dfrac{p_i}{c \, q_i}\}) = P(Y_1 = a_i) \, P(U \leq \dfrac{p_i}{c \, q_i})}}$Donc,
$\displaystyle{\displaylines{ \begin{array}{rcl}P(\{Y_1 = a_i\} \, \text{et} \, \{acceptation\}) & = & P(\{Y_1 = a_i\} \, \text{et} \, \{U \leq \dfrac{p_i}{c \, q_i}\}) \\ \\& = & P(Y_1 = a_i) \, P(U \leq \dfrac{p_i}{c \, q_i}) \\ \\& = & q_i \, \dfrac{p_i}{c \, q_i} \quad (\star) \\ \\& = & \dfrac{p_i}{c}\end{array}}}$
Pour
$\displaystyle{\displaylines{(\star)}}$ on a dans les hypothèses que
$\displaystyle{\displaylines{\dfrac{p_i}{c \, q_i} \leq 1}}$ pour
$\displaystyle{\displaylines{i=1,2,\cdots,n}}$, Donc :
$\displaystyle{\displaylines{P(U \leq \dfrac{p_i}{c \, q_i}) = \int_{0}^{\frac{p_i}{c \, q_i}} 1 \, dt = \dfrac{p_i}{c \, q_i} }}$.
Le cas de l'acceptation vient des événements :
$\displaystyle{\displaylines{\left\{ \{Y_1 = a_1\} \, \text{et} \, \{U \leq \frac{p_1}{c \, q_1}\} \right\}}}$ ou $\displaystyle{\displaylines{\left\{ \{Y_1 = a_2\} \, \text{et} \, \{U \leq \frac{p_2}{c \, q_2}\} \right\}}}$ ou ... ou $\displaystyle{\displaylines{\left\{ \{Y_1 = a_n\} \, \text{et} \, \{U \leq \frac{p_n}{c \, q_n}\} \right\}}}$
Donc on a
$\displaystyle{\displaylines{\{acceptation\} = \left\{\sum_{i=1}^{n} \{Y_1 = a_i\} \, \text{et} \, \{U \leq \frac{p_i}{c \, q_i}\} \right\}}}$Pour
$\displaystyle{\displaylines{i \neq j}}$ on a les événements
$\displaystyle{\displaylines{\left\{ \{Y_1 = a_i\} \, \text{et} \, \{U \leq \frac{p_i}{c \, q_i}\} \right\}}}$ et $\displaystyle{\displaylines{\left\{ \{Y_1 = a_j\} \, \text{et} \, \{U \leq \frac{p_j}{c \, q_j}\} \right\}}}$ sont indépendants. Donc :
$\displaystyle{\displaylines{\begin{array}{rcl}P(acceptation) & = & P\left(\displaystyle\sum_{i=1}^{n} \{Y_1 = a_i\} \, \text{et} \, \{U \leq \dfrac{p_i}{c \, q_i}\}\right) \\ \\& = & \displaystyle\sum_{i=1}^{n} P\left(\{Y_1 = a_i\} \, \text{et} \, \{U \leq \dfrac{p_i}{c \, q_i}\}\right) \\ \\& = & \displaystyle\sum_{i=1}^{n} \dfrac{p_i}{c} \\ \\& = & \dfrac{1}{c}\end{array}}}$
Donc,
$\displaystyle{\displaylines{ \begin{array}{rcl}P(X_1 = a_i) & = & \dfrac{P(\{Y_1 = a_i\} \, \text{et} \, \{acceptation\})}{P(acceptation)} \\ \\& = & \dfrac{p_i}{c} \, c \\ \\& = & P(X=a_i)\end{array}}}$
Résultat: $\displaystyle{\displaylines{X1}}$ est un simulateur de
$\displaystyle{\displaylines{X}}$.
Méthode de composition